Podgląd testu : lo2@sp-05-funkcja-liniowa-pp-5
| Zadanie 1. 1 pkt ⋅ Numer: pp-10808 ⋅ Poprawnie: 199/384 [51%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
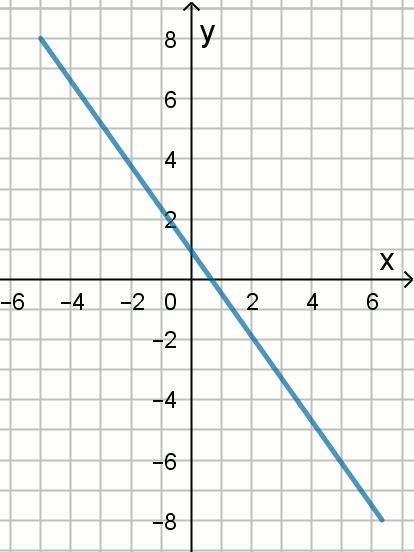
Wskaż wzór tej funkcji:

Odpowiedzi:
| A. y=-\frac{\sqrt{2}}{2}x+1 | B. y=-\sqrt{2}x+1 |
| C. y=\frac{1}{\sqrt{2}}x+1 | D. y=\sqrt{2}x+1 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10796 ⋅ Poprawnie: 152/254 [59%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Liczba 8 jest miejscem zerowym funkcji określonej wzorem
f(x)=\left(1+\frac{a}{8}\right)x+2.
Wyznacz a.
Odpowiedź:
| a= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10899 ⋅ Poprawnie: 85/117 [72%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Punkty o współrzędnych (800,200) oraz
(900,-600) należą do wykresu funkcji liniowej
y=mx+n.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : z treści wynika, że m \lessdot 0 | T/N : z treści wynika, że n \lessdot 0 |
| T/N : z treści wynika, że n=0 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10924 ⋅ Poprawnie: 60/80 [75%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Funkcja liniowa f określona jest wzorem
f(x)=ax+b i spełnia warunek f(7)-f(4)=21.
Wyznacz a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10925 ⋅ Poprawnie: 82/105 [78%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wykres funkcji liniowej
f(x)=\left(\frac{1}{2}m-6\right)x+\frac{1}{2}m+1
zawiera punkt M=(0,1).
Wyznacz m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20309 ⋅ Poprawnie: 233/300 [77%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
» Oblicz miejsce zerowe funkcji
f(x)=
\begin{cases}
-1+2x \text{, dla } x\leqslant 2 \\
x \text{, dla } x > 2
\end{cases}
.
Odpowiedź:
| x= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20298 ⋅ Poprawnie: 223/633 [35%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Funkcja liniowa f określona jest wzorem
f(x)=mx-n. Wiadomo, że
f(5)=5, oraz, że do wykresu funkcji
f należy punkt P=(1,1).
Wyznacz m.
Odpowiedź:
| m= | |
Podpunkt 7.2 (1 pkt)
Wyznacz n.
Odpowiedź:
| n= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20310 ⋅ Poprawnie: 88/137 [64%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Rozwiąż równanie
\frac{x+10}{4x+8}=-2
.
Odpowiedź:
| x= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20303 ⋅ Poprawnie: 88/137 [64%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Zależność temperatury w skali Fahrenheita \ ^{\circ}{F}
od temperatury w skali Celsjusza \ ^{\circ}{C} wyraża
wzór f(c)=32+1,8\cdot c, gdzie
f – temperatura w skali Fahrenheita, zaś
c – temperatura w skali Celsjusza.
Oblicz, w jakiej temperaturze w skali Fahrenheita zażywasz kąpieli, jeśli termometr wskazuje, że temperatura wody wynosi wtedy 42^{\circ}C.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 9.2 (1 pkt)
W czajniku znajduje się woda o temperaturze
117^{\circ}F.
Jaką temperaturę w stopniach Celsjusza ma ta woda?
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 10. 4 pkt ⋅ Numer: pp-30056 ⋅ Poprawnie: 26/66 [39%] | Rozwiąż |
Podpunkt 10.1 (4 pkt)
« Z miejscowości A wyjechał autobus osobowy i dotarł
do miejscowości B po
t godzinach jazdy. Godzinę póżniej od autobusu
osobowego na tę samą trasę wyjechał autobus pospieszny i dotarł do miejscowości
B o godzinę wcześniej niż autobus osobowy.
Po ilu godzinach swojej jazdy autobus pospieszny wyprzedził autobus osobowy?
Dane
t=8
Odpowiedź:
| t\ [h]= | |