⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-05-funkcja-liniowa-pr-3
| Zadanie 1. 1 pkt ⋅ Numer: pr-10104 ⋅ Poprawnie: 10/17 [58%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
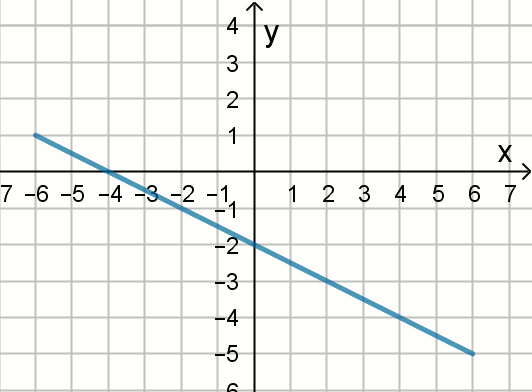
Na rysunku poniżej przedstawiony jest fragment wykresu funkcji liniowej
y=ax+b.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : a > -1 \wedge b \lessdot -1 | T/N : a \lessdot -1 \wedge b \lessdot -1 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11418 ⋅ Poprawnie: 191/313 [61%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Punkty A=(2,1) i
B=(-3,6) należą do prostej
k.
Prosta l symetryczna do prostej
k względem początku układu współrzędnych
ma równanie y=ax+b.
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10903 ⋅ Poprawnie: 211/346 [60%] | Rozwiąż |
Podpunkt 3.1 (0.8 pkt)
Funkcja liniowa f(x)=(-7-3m)x+1-6m jest rosnąca, gdy
parametr m należy do pewnego przedziału.
Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| \frac{k}{n}= | |
Podpunkt 3.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 5 | B. +\infty |
| C. 7 | D. -8 |
| E. -\infty | F. 0 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10887 ⋅ Poprawnie: 214/297 [72%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wykresy funkcji liniowych opisanych wzorami
f(x)=x+\frac{5}{4} i
g(x)=7 opisują proste:
Odpowiedzi:
| A. przecinające się pod kątem o mierze 90^{\circ} | B. pokrywające się |
| C. równoległe i różne | D. przecinające się pod kątem różnym od 90^{\circ} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10942 ⋅ Poprawnie: 161/261 [61%] | Rozwiąż |
Podpunkt 5.1 (0.8 pkt)
Dana jest funkcja liniowa
g(x)=\frac{2}{9}+\frac{1}{6}x
.
Funkcja g przyjmuje wartości ujemne dla argumentów
należących do pewnego przedziału.
Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| \frac{m}{n}= | |
Podpunkt 5.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -5 | B. -\infty |
| C. +\infty | D. -8 |
| E. 8 | F. -1 |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20844 ⋅ Poprawnie: 114/332 [34%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Punkt K=(-2,6) należy do wykresu funkcji
liniowej określonej wzorem f(x)=(-8-m)x+4.
Wyznacz m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Wykresy funkcji f i funkcji określonej wzorem
h(x)=2-2x przecinają oś
Ox w tym samym punkcie.
Podaj m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20840 ⋅ Poprawnie: 156/279 [55%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Funkcja liniowa f określona wzorem
f(x)=mx+n wartości nieujemne przyjmuje tylko
w przedziale (-\infty, 2\rangle oraz zachodzi
warunek f(-4)=18. Wyznacz wartości współczynników
m i n.
Podaj m.
Odpowiedź:
| m= | |
Podpunkt 7.2 (1 pkt)
Podaj n.
Odpowiedź:
| n= | |
| Zadanie 8. 2 pkt ⋅ Numer: pr-20032 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=ax+b. Dla a=798
i b=799 oblicz
\frac{f(799)}{799^2}.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Narysuj w układzie współrzędnych zbiór
A=\left\{(x,y): x\in\langle 1,3\rangle \wedge y=-\frac{1}{2}x+b \wedge b\in\langle -2,1\rangle\right\}
.
Podaj współrzędną y tego punktu należącego do zbioru A, który jest najbardziej oddalony od początku układu współrzędnych.
Odpowiedź:
| y= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20310 ⋅ Poprawnie: 88/137 [64%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Rozwiąż równanie
\frac{8x-5}{8x-4}=10
.
Odpowiedź:
| x= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20301 ⋅ Poprawnie: 164/381 [43%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
Trójkąt ograniczony osiami układu i prostą o równaniu
4y=-10x-10 ma pole powierzchni równe
P.
Oblicz P.
Odpowiedź:
| P_{\triangle}= | |
| Zadanie 11. 4 pkt ⋅ Numer: pp-30049 ⋅ Poprawnie: 38/68 [55%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
« Rozwiąż nierówność\frac{(x-1)^2}{3}-\frac{33}{2}<=\frac{16}{9}x-\frac{1-x}{2}\cdot \left(\frac{2}{3}x+3\right).
Podaj najmniejszą liczbe spęłniającą tę nierówność.
Odpowiedź:
| min= | |
Podpunkt 11.2 (2 pkt)
Najmniejszą liczbę spęłniającą tę nierówność zapisz w postaci ułamka
nieskracalnego o dodatnim mianowniku.
Podaj mianownik tego ułamka.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 12. 4 pkt ⋅ Numer: pp-30058 ⋅ Poprawnie: 41/63 [65%] | Rozwiąż |
Podpunkt 12.1 (4 pkt)
» Pan Kowalski wykonuje pewną pracę w ciągu p
godzin. Tę samą pracę pan Nowak wykonuje w ciągu q
godzin.
Ile godzin potrzeba, aby panowie pracując razem wykonali tę samą pracę.
Dane
p=28
q=21
q=21
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)