⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-06-ukl-row-lin-pp-6
| Zadanie 1. 1 pkt ⋅ Numer: pp-10851 ⋅ Poprawnie: 158/250 [63%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
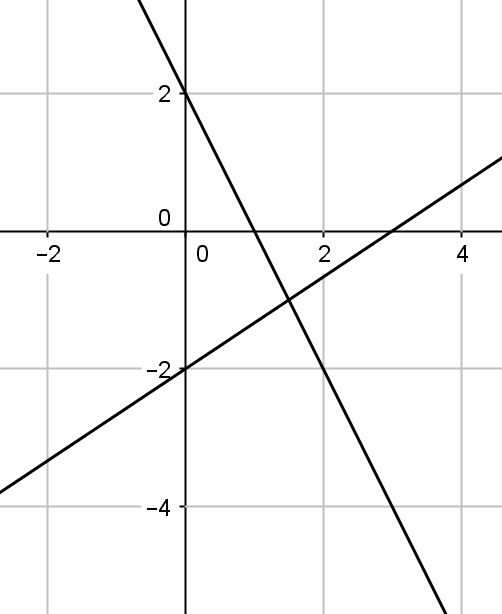
Wskaż parę prostych widocznych na rysunku:
Odpowiedzi:
| A. y=-2x+2\wedge y=\frac{3}{2}x-2 | B. y=-2x-2\wedge y=\frac{3}{2}x+2 |
| C. y=-2x-2\wedge y=\frac{2}{3}x+2 | D. y=-2x+2\wedge y=\frac{2}{3}x-2 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11694 ⋅ Poprawnie: 42/103 [40%] | Rozwiąż |
Podpunkt 2.1 (0.5 pkt)
Rozwiąż układ równań metodą przeciwnych współczynników:
\begin{cases}
\frac{2}{5}x+\frac{1}{3}y=\frac{37}{15} \\
\frac{1}{2}x-\frac{2}{9}y=-\frac{1}{9}
\end{cases}
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (0.5 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10853 ⋅ Poprawnie: 536/703 [76%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Ile rozwiązań ma układ równań
\begin{cases}
-\frac{1}{2}x-\frac{1}{2}y=-1 \\
x+y=1
\end{cases}
:
Odpowiedzi:
| A. 0 | B. 2 |
| C. nieskończenie wiele | D. 1 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11701 ⋅ Poprawnie: 30/38 [78%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wyznacz wartości parametrów m i n tak,
aby pary liczb (-15,m+4) i
(n-14,18) spełniały równanie
\frac{3}{10}x-\frac{1}{2}y=-6.
Podaj liczby m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (wpisz liczbę całkowitą) | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10948 ⋅ Poprawnie: 98/154 [63%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Wykres funkcji liniowej y=mx+6 wraz z osiami
układu współrzędnych ograniczają trójkąt o polu powierzchni równym
30.
Wyznacz najmniejsze możliwe i największe możliwe m.
Odpowiedzi:
| m_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| m_{max} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20837 ⋅ Poprawnie: 221/396 [55%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Rozwiąż układ równań
\begin{cases}
\frac{1}{3}(x-2y)-x=2-\frac{1}{2}(x+2y-2) \\
\frac{1}{2}(x-10)-\frac{1}{4}(2y-12)=x+2y
\end{cases}
.
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20321 ⋅ Poprawnie: 516/895 [57%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Rozwiąż układ równań
\begin{cases}
x+0,75y=-6 \\
0,25y=2x+19
\end{cases}
.
Podaj sumę x^2+y^2.
Odpowiedź:
x^2+y^2=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20326 ⋅ Poprawnie: 637/941 [67%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Kinga jest o 8 lat starsza od Kamila.
2 lat temu Kamil był dwa razy młodszy pod Kingi.
Ile lat ma teraz Kamil.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Ile lat ma teraz Kinga.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20330 ⋅ Poprawnie: 498/715 [69%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Suma cyfr liczby dwucyfrowej jest równa 12.
Jeśli od cyfry dziesiątek odejmiemy 6, a do cyfry
jedności dodamy 6, to otrzymana liczba będzie się
składać z takich samych cyfr, ale zapisanych w odwrotnej kolejności.
Wyznacz tę liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 10. 4 pkt ⋅ Numer: pp-30055 ⋅ Poprawnie: 27/125 [21%] | Rozwiąż |
Podpunkt 10.1 (4 pkt)
« Dane są funkcje
f(x)=
\begin{cases}
-2 \text{, dla } x \lessdot 4 \\
x-6\text{, dla } x\geqslant 4
\end{cases}
oraz g(x)=\frac{1}{3}x+\frac{a}{3}.
Oblicz pole powierzchni figury ograniczonej wykresami tych funkcji.
Dane
a=2
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)