Podgląd testu : lo2@sp-08-planimetria-pp-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10480 ⋅ Poprawnie: 375/476 [78%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Suma miar kątów n kąta jest równa
3060^{\circ}.
Wyznacz n.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 7, 7, 10 | T/N : \sqrt{10}, \sqrt{6}, \sqrt{5} |
| T/N : 4, 5, 6 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10601 ⋅ Poprawnie: 640/862 [74%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Odcinki BC i EF
na rysunku są równoległe, przy czym
|AC|=\frac{5}{2} i
|BC|=11:
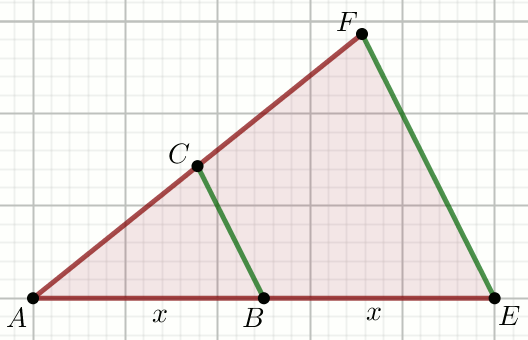

Oblicz długość odcinka EF.
Odpowiedź:
|EF|=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10604 ⋅ Poprawnie: 186/262 [70%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{6},
|DC|=\frac{5}{12} i
|DE|=\frac{5}{12}:
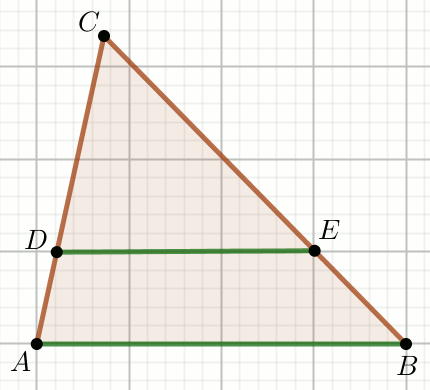

Oblicz długość odcinka AB.
Odpowiedź:
| |AB|= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10596 ⋅ Poprawnie: 219/351 [62%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Odcinki DE i AB
są równoległe, przy czym
|DE|=\frac{1}{6} i
|AB|=\frac{5}{12}:
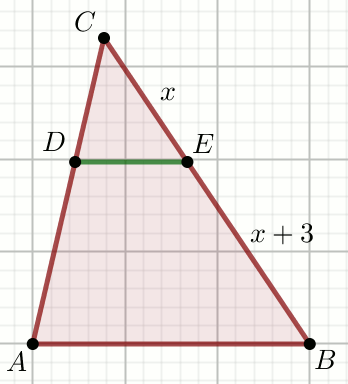

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11522 ⋅ Poprawnie: 572/1180 [48%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
(1 pkt)
W trójkącie prostokątnym ABC przyprostokątna
AC ma długość \sqrt{13}, a wysokość
AD opuszczona z wierzchołka kąta prostego
A ma długość 2:
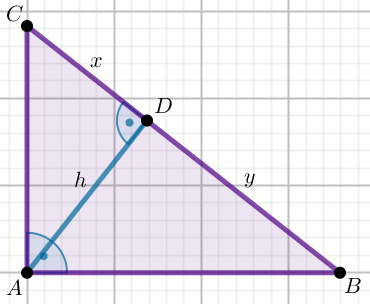

Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle ABC}= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10578 ⋅ Poprawnie: 111/249 [44%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
W trójkącie równoramiennym ABC o wysokościach
CD i AE podstawa
AB ma długość 20,
a odcinek BE ma długość
\frac{100}{13}.
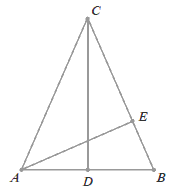

Oblicz długość odcinka CD.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-10584 ⋅ Poprawnie: 391/480 [81%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Przedstawione na rysunku trójkąty ABC i
PQR są podobne.

Oblicz długość boku AB trójkąta ABC.

Odpowiedź:
| |AB|= | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10790 ⋅ Poprawnie: 243/369 [65%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
» Punkty o współrzędnych A=(-4,-6),
B=(-5,-4) i C=(-3,2) są
wierzchołkami trójkąta.
Oblicz długość środkowej AD tego trójkąta.
Odpowiedź:
| |AD|= | ||
| (wpisz trzy liczby całkowite) | ||