Podgląd testu : lo2@sp-08-planimetria-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-11567 ⋅ Poprawnie: 48/77 [62%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Z punktu leżącego na zewnątrz kąta ABC o mierze
58^{\circ} poprowadzono prostą równoległą do półprostej
BA^{\rightarrow} oraz prostą prostopadłą do półprostej
BC^{\rightarrow}.
Podaj miarę stopniową większego z kątów, pod jakimi przecinają się te proste.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11566 ⋅ Poprawnie: 36/66 [54%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Kąt zewnętrzny wielokąta foremnego ma miarę 20^{\circ}.
Ile przekątnych ma ten wielokąt?
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 8, 4, 4\sqrt{5} | T/N : 4+4\sqrt{2}, -4+4\sqrt{2}, 8\sqrt{2} |
| T/N : 16, 20, 24 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11383 ⋅ Poprawnie: 645/838 [76%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Odcinek AB o długości 18 jest
równoległy do odcinka CD, przy czym:
|PA|=7 i
|AC|=14:
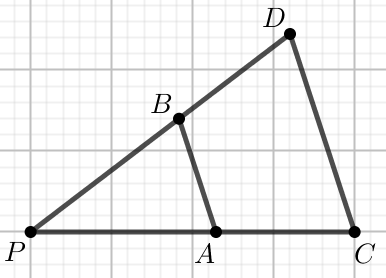

Oblicz długość odcinka CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10594 ⋅ Poprawnie: 145/235 [61%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
W trójkącie ABC poprowadzono odcinek
DE równoległy do boku AB, przy czym
|AB|=\frac{21}{4} i
|BE|:|EC|=6:
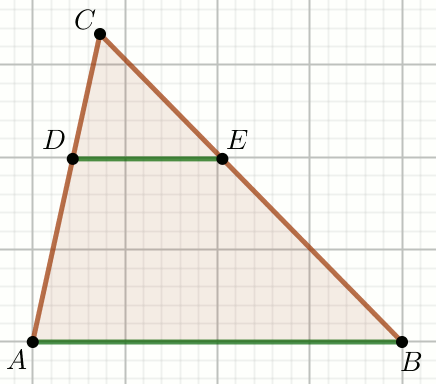

Oblicz długość odcinka DE.
Odpowiedź:
| |DE|= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10595 ⋅ Poprawnie: 273/425 [64%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AP|=\frac{5}{4},
|BP|=\frac{4}{3} i
|CP|=\frac{15}{4}:
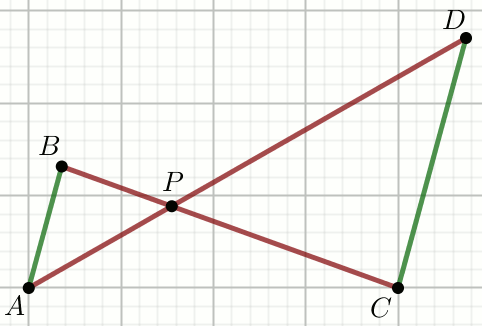

Oblicz długość odcinka DP.
Odpowiedź:
| |DP|= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11568 ⋅ Poprawnie: 36/58 [62%] | Rozwiąż |
Podpunkt 7.1 (0.5 pkt)
W trapezie podstawy mają długość 2 i
8, a wysokość ma długość 6.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 7.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11522 ⋅ Poprawnie: 572/1180 [48%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
(1 pkt)
W trójkącie prostokątnym ABC przyprostokątna
AC ma długość \sqrt{85}, a wysokość
AD opuszczona z wierzchołka kąta prostego
A ma długość 6:
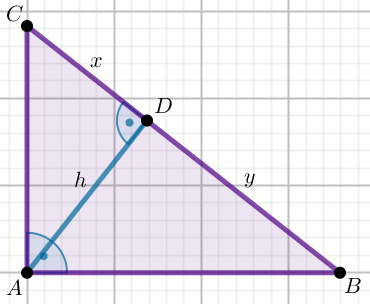

Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle ABC}= | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11583 ⋅ Poprawnie: 10/55 [18%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
«« Punkty E i F dzielą
przyprostokątne trójkąta ABC w stosunku:
|CE|:|CA|=|BF|:|BA|=\frac{1}{5}, przy czym:
P_{\triangle MCE}=4 i
P_{\triangle NFB}=4:
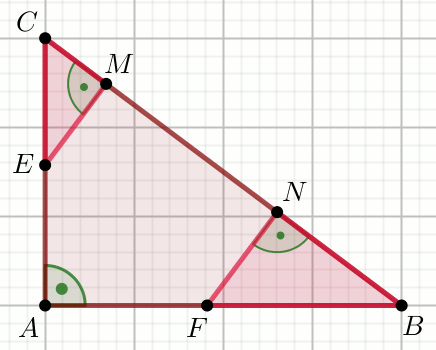

Oblicz pole powierzchni trójkąta ABC.
Odpowiedź:
P_{\triangle ABC}=
(wpisz liczbę całkowitą)
| Zadanie 10. 1 pkt ⋅ Numer: pp-10578 ⋅ Poprawnie: 111/249 [44%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
W trójkącie równoramiennym ABC o wysokościach
CD i AE podstawa
AB ma długość 80,
a odcinek BE ma długość
\frac{1600}{29}.
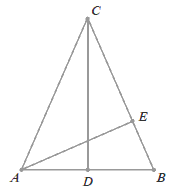

Oblicz długość odcinka AC.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pp-10664 ⋅ Poprawnie: 97/158 [61%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Kąt trójkąta prostokątnego ma miarę 77^{\circ}.
Z wierzchołka kąta prostego poprowadzono środkową i wysokość tego trójkąta.
Oblicz miarę stopniową kąta między nimi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. 1 pkt ⋅ Numer: pp-11510 ⋅ Poprawnie: 577/879 [65%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Punkt S=(4,-2) jest środkiem odcinka
AB takiego, że punkt A=(x_A, y_A)
należy do osi Oy, a punkt B=(x_B, y_B)
należy do osi Ox.
Wyznacz współrzędne y_A i x_B.
Odpowiedzi:
| y_A | = |
(wpisz liczbę całkowitą) |
| x_B | = |
(wpisz liczbę całkowitą) |