Podgląd testu : lo2@sp-08-planimetria-pp-4
| Zadanie 1. 1 pkt ⋅ Numer: pp-11567 ⋅ Poprawnie: 48/77 [62%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Z punktu leżącego na zewnątrz kąta ABC o mierze
64^{\circ} poprowadzono prostą równoległą do półprostej
BA^{\rightarrow} oraz prostą prostopadłą do półprostej
BC^{\rightarrow}.
Podaj miarę stopniową większego z kątów, pod jakimi przecinają się te proste.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11462 ⋅ Poprawnie: 195/348 [56%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, 2+\sqrt{3}, jest:
Odpowiedzi:
| A. jest rozwartokątny | B. jest ostrokątny |
| C. nie istnieje | D. jest prostokątny |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10600 ⋅ Poprawnie: 326/462 [70%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Odcinki DE i AB są
równoległe, przy czym
|CD|=1 i
|CE|=\frac{17}{12}:
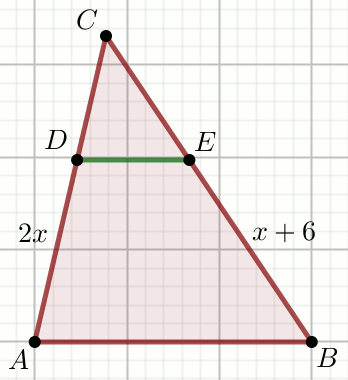

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10585 ⋅ Poprawnie: 264/397 [66%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Przedstawione na rysunku trójkąty są podobne.
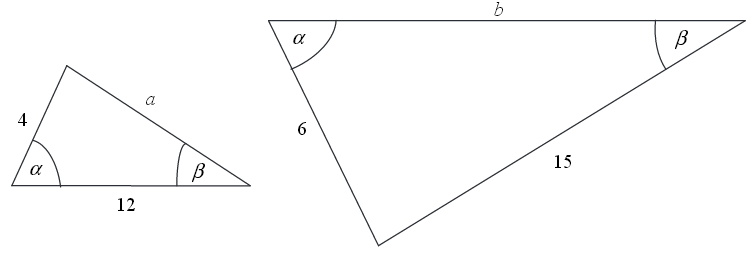

Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11394 ⋅ Poprawnie: 208/324 [64%] | Rozwiąż |
Podpunkt 5.1 (0.5 pkt)
Dany jest punkt B=(5,-2) oraz wektor
\overrightarrow{AB}=[1, -3]. Wyznacz środek odcinka S_{AB}=(x_S, y_S).
Podaj x_S.
Odpowiedź:
| x_S= | |
Podpunkt 5.2 (0.5 pkt)
Podaj y_S.
Odpowiedź:
| y_S= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20780 ⋅ Poprawnie: 70/218 [32%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« W trójkącie ABC dane są:
A=(8,3), B=(-1,2)
i C=(3,-2). Oblicz długości boków tego trójkąta.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle ABC}= | |
Podpunkt 6.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pp-20246 ⋅ Poprawnie: 80/121 [66%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Odcinki AD i BE
przecinają się w punkcie C. W trójkątach
ABC i CDE zachodzą
związki: |\sphericalangle CAB|=|\sphericalangle CED|,
|AC|=5, |BC|=3,
|CE|=10, jak na rysunku.
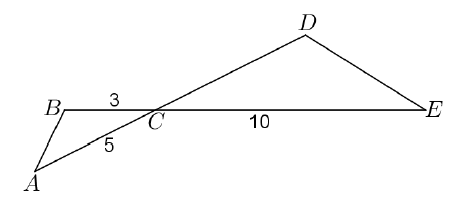

Oblicz długość boku CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20251 ⋅ Poprawnie: 75/238 [31%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{35}{4},
|AB|=14,
|AD|=7 i
|BC|=\frac{21}{4}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
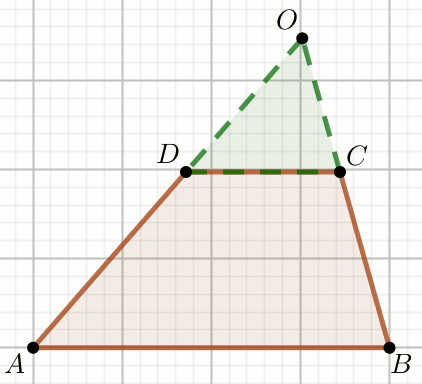
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.

Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20709 ⋅ Poprawnie: 77/246 [31%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Dane są długości boków trójkąta 117,
180 i 189. Zbadaj, czy
trójkąt ten jest prostokątny, ostrokątny czy rozwartokątny.
Jeśli trójkąt jest prostokątny wpisz 1, jeśli ostrokątny wpisz 2, jeśli rozwartokątny wpisz 3.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
Wyznacz długość wysokości opuszczonej na najdłuższy bok tego trójkąta.
Odpowiedź:
| h= | ||
| (wpisz trzy liczby całkowite) | ||