Podgląd testu : lo2@sp-08-planimetria-pp-6
| Zadanie 1. 1 pkt ⋅ Numer: pp-11566 ⋅ Poprawnie: 36/66 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Kąt zewnętrzny wielokąta foremnego ma miarę 40^{\circ}.
Ile przekątnych ma ten wielokąt?
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10583 ⋅ Poprawnie: 281/376 [74%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Trójkąt równoramienny prostokątny ma przeciwprostokątną długości
6+8\sqrt{2}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 3. 1 pkt ⋅ Numer: pp-10602 ⋅ Poprawnie: 477/703 [67%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zielone odcinki na rysunku sa równolegle, przy czym
|AP|=1,
|BP|=\frac{1}{2},
|CP|=\frac{3}{2},
|DP|=3,
|AB|=\frac{7}{4}:
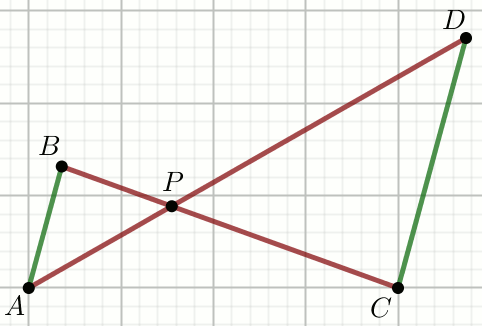

Oblicz długość odcinka CD.
Odpowiedź:
| |CD|= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11568 ⋅ Poprawnie: 36/58 [62%] | Rozwiąż |
Podpunkt 4.1 (0.5 pkt)
W trapezie podstawy mają długość 1 i
8, a wysokość ma długość 6.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 4.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11394 ⋅ Poprawnie: 208/324 [64%] | Rozwiąż |
Podpunkt 5.1 (0.5 pkt)
Dany jest punkt B=(5,1) oraz wektor
\overrightarrow{AB}=[1, -3]. Wyznacz środek odcinka S_{AB}=(x_S, y_S).
Podaj x_S.
Odpowiedź:
| x_S= | |
Podpunkt 5.2 (0.5 pkt)
Podaj y_S.
Odpowiedź:
| y_S= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20876 ⋅ Poprawnie: 10/22 [45%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Trzy liczby x+12, -6-x i
4x+52 są długościami boków trójkąta, gdy liczba liczba
x należy do przedziału (p,q).
Podaj liczbę p.
Odpowiedź:
| p= | |
Podpunkt 6.2 (1 pkt)
Podaj liczbę q.
Odpowiedź:
| q= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20725 ⋅ Poprawnie: 33/241 [13%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Trójkąt ABC na rysunku jest równoramienny, a
zielony czworokąt jest kwadratem, przy czym |AB|=12 i
|BC|=10:
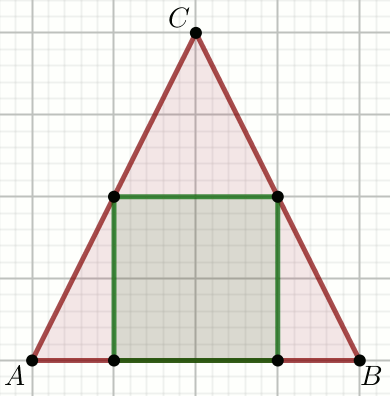

Oblicz pole powierzchni tego kwadratu.
Odpowiedź:
| P_{\square}= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20243 ⋅ Poprawnie: 98/237 [41%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Boki trójkąta prostokątnego mają długości: a,
6 i 13.
Podaj najmniejszą możliwą wartość a.
Odpowiedź:
a_{min}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (1 pkt)
Podaj największą możliwą wartość a.
Odpowiedź:
a_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20251 ⋅ Poprawnie: 75/238 [31%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=5,
|AB|=8,
|AD|=4 i
|BC|=3.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
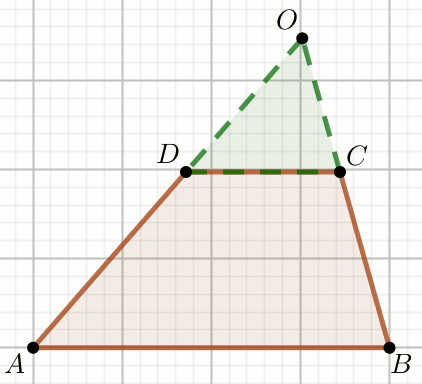
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.

Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20244 ⋅ Poprawnie: 59/154 [38%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
W trójkącie prostokątnym najkrótszy bok ma długość \frac{13}{2}, a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o \frac{1}{2}.
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
| max= | |
Podpunkt 10.2 (1 pkt)
Oblicz odległość punktu przecięcia się środkowych tego trójkąta od
wierzchołka kąta prostego.
Odpowiedź:
| d= | |
| Zadanie 11. 4 pkt ⋅ Numer: pp-30301 ⋅ Poprawnie: 25/71 [35%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
«« Trójkąt na rysunku jest równoramienny o podstawie AB
o długości |AB|=30 i ramieniu |BC|=113:
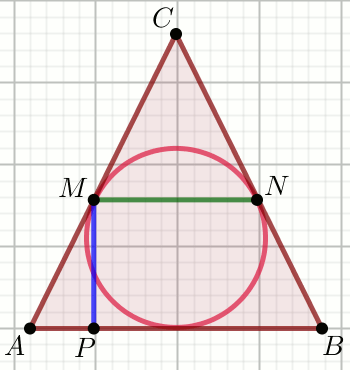

Oblicz |MN|.
Odpowiedź:
| |MN|= | |
Podpunkt 11.2 (2 pkt)
Oblicz |MP|.
Odpowiedź:
| Wpisz odpowiedź: | |