Podgląd testu : lo2@sp-08-planimetria-pr-3
| Zadanie 1. 1 pkt ⋅ Numer: pr-10374 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Różnica liczby boków dwóch wielokątów jest równa jeden, a różnica ilości ich przekątnych
jest równa 27 boków.
Ile boków ma wielokąt o mniejszej liczbie boków?
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11462 ⋅ Poprawnie: 195/349 [55%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, 2+\sqrt{2}, jest:
Odpowiedzi:
| A. jest ostrokątny | B. jest prostokątny |
| C. jest rozwartokątny | D. nie istnieje |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10600 ⋅ Poprawnie: 326/462 [70%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Odcinki DE i AB są
równoległe, przy czym
|CD|=\frac{17}{12} i
|CE|=1:
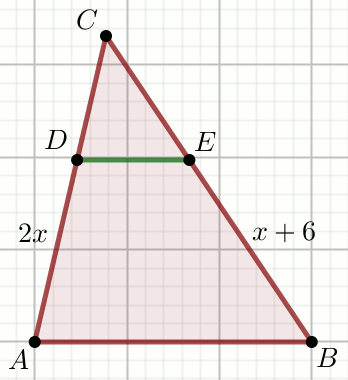

Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10578 ⋅ Poprawnie: 111/249 [44%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
W trójkącie równoramiennym ABC o wysokościach
CD i AE podstawa
AB ma długość 40,
a odcinek BE ma długość
\frac{200}{13}.
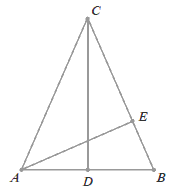

Oblicz długość odcinka CD.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pr-11596 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wektory
\vec{u}=[2m+n-15, m-3n-9]
oraz
\vec{v}=[m, -n+8] są równe.
Wyznacz wartości parametrów m i n
Odpowiedzi:
| m | = |
(wpisz liczbę zapisaną dziesiętnie) |
| n | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. 2 pkt ⋅ Numer: pr-20573 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Dane sa wektory:
\vec{a}=[a_x, a_y],
\vec{b}=[b_x, b_y] i
\vec{c}=[c_x, c_y].
Wyznacz liczby rzeczywiste i p i
q takie, że
p\cdot\vec{a}+q\cdot\vec{b}=\vec{c}.
Podaj p.
Dane
a_x=-1
a_y=2
b_x=-1
b_y=3
c_x=9
c_y=-5
a_y=2
b_x=-1
b_y=3
c_x=9
c_y=-5
Odpowiedź:
| p= | |
Podpunkt 6.2 (1 pkt)
Podaj q.
Odpowiedź:
| q= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20722 ⋅ Poprawnie: 69/145 [47%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
» Trójkąt na rysunku jest równoramienny o podstawie
AB, przy czym |CD|=\frac{238}{13} oraz
|DB|=\frac{100}{13}:
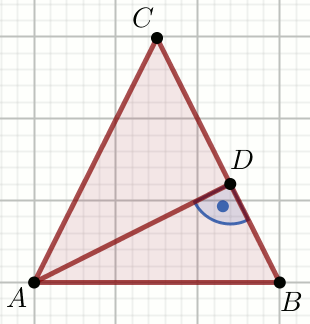

Oblicz |AB|.
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 8. 2 pkt ⋅ Numer: pr-20027 ⋅ Poprawnie: 1/1 [100%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Przeciwprostokątna trójkąta prostokątnego ma długość
205, a jedna z przyprostokątnych jest o
23 dłuższa od drugiej.
Oblicz obwód tego trójkąta.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20863 ⋅ Poprawnie: 40/169 [23%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
(2 pkt)
W trójkącie równoramiennym ABC dane są długości boków:
|AC|=|BC|=70 i |AB|=84.
Na przedłużeniu boku AB zaznaczono taki punkt D,
że |DB|=147. Przez punkt A
poprowadzono prostą równoległą do boku BC, która przecięła odcinek
DC w punkcie E (zobacz rysunek):
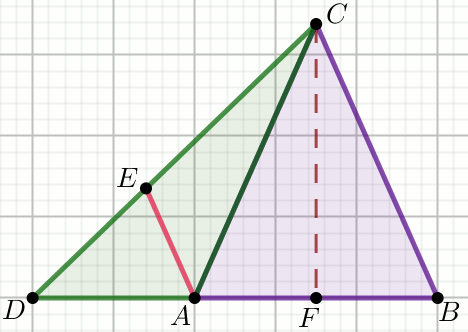

Oblicz |DE|.
Odpowiedź:
| |DE|= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20234 ⋅ Poprawnie: 51/183 [27%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Z wierzchołków kątów ostrych trójkąta prostokątnego poprowadzono dwie
środkowe o długościach 5 i
6.
Podaj długość krótszej z przyprostokątnych tego trójkąta.
Odpowiedź:
min=
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (1 pkt)
Podaj długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
c=
(liczba zapisana dziesiętnie)
| Zadanie 11. 4 pkt ⋅ Numer: pp-30301 ⋅ Poprawnie: 25/71 [35%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
«« Trójkąt na rysunku jest równoramienny o podstawie AB
o długości |AB|=22 i ramieniu |BC|=61:
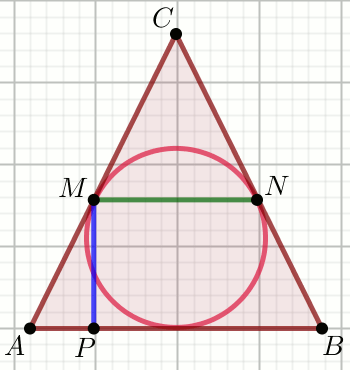

Oblicz |MN|.
Odpowiedź:
| |MN|= | |
Podpunkt 11.2 (2 pkt)
Oblicz |MP|.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 12. 4 pkt ⋅ Numer: pp-30135 ⋅ Poprawnie: 72/127 [56%] | Rozwiąż |
Podpunkt 12.1 (4 pkt)
« Punkt E jest środkiem przeciwprostokątnej
AB trójkąta ABC.
Odcinek DE ma długość 1, jak na rysunku.
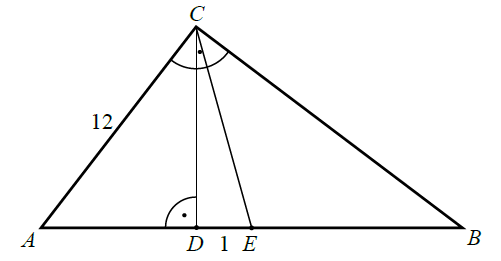
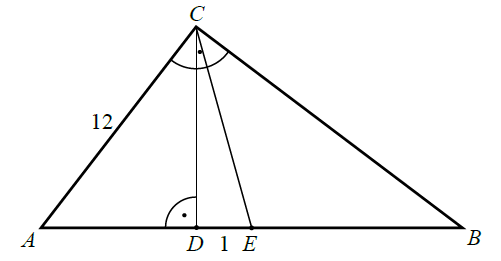
Oblicz obwód trójkąta ABC.
Odpowiedź:
L_{\triangle ABC}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)