⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-09-trygonom-1-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10631 ⋅ Poprawnie: 374/652 [57%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wiadomo, że kąt \alpha jest ostry oraz
\sin\alpha=\frac{5\sqrt{29}}{29}.
Oblicz wartość wyrażenia \sin \alpha-\cos\alpha.
Odpowiedź:
| \sin\alpha-\cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-10614 ⋅ Poprawnie: 689/1065 [64%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Kąt \alpha jest kątem ostrym oraz
\tan\alpha=\frac{9}{5}.
Oblicz wartość wyrażenia w=\frac{3\cos\alpha-2\sin\alpha}{\sin\alpha-5\cos\alpha}.
Odpowiedź:
| w= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10609 ⋅ Poprawnie: 609/829 [73%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Kąt \alpha jest ostry i
\sin \alpha=\frac{1}{17}.
Wówczas:
Odpowiedzi:
| A. \cos\alpha=\frac{\sqrt{290}}{17} | B. \cos\alpha \lessdot \frac{\sqrt{287}}{17} |
| C. \cos\alpha > \frac{\sqrt{287}}{17} | D. \cos\alpha=\frac{\sqrt{287}}{17} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10663 ⋅ Poprawnie: 409/675 [60%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Trójkąt ABC jest prostokątny, a kąt
BCA jest prosty. Wiadomo, że
\cos\sphericalangle CAB=\frac{20}{29} i
|AB|=29.
Oblicz długość boku BC.
Odpowiedź:
| |BC|= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10651 ⋅ Poprawnie: 346/498 [69%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
W trapezie prostokątnym kąt ostry ma miarę
60^{\circ}, a podstawy mają długości
6 i 13.
Oblicz długość wysokości tego trapezu.
Odpowiedź:
| h= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. 1 pkt ⋅ Numer: pp-10662 ⋅ Poprawnie: 350/486 [72%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Zapisz obwód trójkąta ABC w postaci p\cdot a:
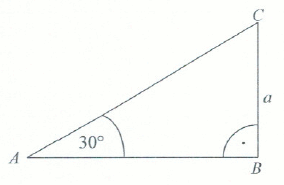
Podaj p.
Odpowiedź:
p=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 7. 1 pkt ⋅ Numer: pp-10623 ⋅ Poprawnie: 114/183 [62%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Wiadomo, że \alpha i \beta
są miarami kątów ostrych trójkąta prostokątnego oraz
100\sin^2\alpha+\cos^2\beta=1.
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10630 ⋅ Poprawnie: 198/462 [42%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Kąty \alpha i \beta
trójkata prostokątnego są ostre. Wówczas wyrażenie
\frac{6\cos\alpha\cdot (3-3\sin^2\beta)\cdot \tan\alpha}
{5\sin^2\alpha\cdot \cos\beta}
jest równe:
Odpowiedzi:
| A. \frac{18}{5} | B. \frac{18}{5}\cos\alpha |
| C. \frac{6}{5}\sin\alpha | D. \frac{18}{5}\tan\alpha |