⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-09-trygonom-1-pp-5
| Zadanie 1. 1 pkt ⋅ Numer: pp-10631 ⋅ Poprawnie: 374/652 [57%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wiadomo, że kąt \alpha jest ostry oraz
\sin\alpha=\frac{\sqrt{26}}{26}.
Oblicz wartość wyrażenia \sin \alpha-\cos\alpha.
Odpowiedź:
| \sin\alpha-\cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-10670 ⋅ Poprawnie: 327/573 [57%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Trapez na rysunku jest prostokątny:
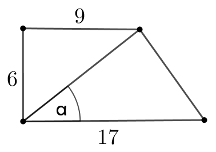
Miara kąta \alpha spełnia warunek:
Odpowiedzi:
| A. 30^{\circ} \lessdot \alpha < 35^{\circ} | B. \alpha=30^{\circ} |
| C. 50^{\circ} \lessdot \alpha < 60^{\circ} | D. \alpha=45^{\circ} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10657 ⋅ Poprawnie: 572/669 [85%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Przyprostokątne w trójkącie prostokątnym mają długości
1 oraz
\sqrt{3}.
Wyznacz miarę stopniową najmniejszego kąta w tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10611 ⋅ Poprawnie: 237/485 [48%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Kąt \alpha jest ostry oraz
\tan\alpha=\frac{6}{5}.
Oblicz wartość wyrażenia \frac{2-\cos\alpha}{2+\cos\alpha}.
Odpowiedź:
| \frac{2-\cos\alpha}{2+\cos\alpha}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 5. 1 pkt ⋅ Numer: pp-10644 ⋅ Poprawnie: 349/458 [76%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wiadomo, że 0^{\circ}\lessdot \alpha <90^{\circ} oraz
\tan \alpha=10\sin\alpha.
Oblicz \cos\alpha.
Odpowiedź:
| \cos\alpha= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20733 ⋅ Poprawnie: 111/396 [28%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Wyznacz wysokości trójkata ABC, w którym a=48
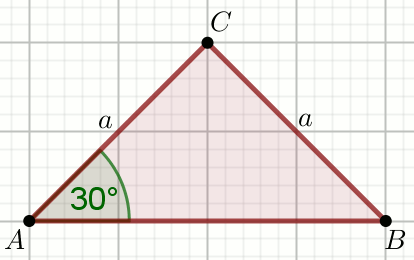
Podaj długość najkrótszej z wysokości tego trójkąta.
Odpowiedź:
| h_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 6.2 (1 pkt)
Podaj długość najdłuższej z wysokości tego trójkąta.
Odpowiedź:
| h_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pp-20254 ⋅ Poprawnie: 107/202 [52%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Kąt \beta jest ostry. Oblicz wartość wyrażenia
\sin^2\beta-3\cos^2\beta.
Dane
\sin\beta=\frac{\sqrt{3}}{10}=0.17320508075689
Odpowiedź:
| \sin^2\beta-3\cos^2\beta= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20282 ⋅ Poprawnie: 84/172 [48%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
W trójkącie prostokątnym ABC kąt przy wierzchołku
A jest prosty, a kąt przy wierzchołku
B ma miarę \beta.
Oblicz \tan \beta.
Dane
\sin\beta=\frac{1}{11}=0.09090909090909
Odpowiedź:
| \tan\beta= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 9. 2 pkt ⋅ Numer: pp-20267 ⋅ Poprawnie: 123/251 [49%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Oblicz wartość wyrażenia
\left(\frac{1}{9}-\frac{1}{9}\sin^2\alpha\right)(1+\tan^2\alpha)
.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20737 ⋅ Poprawnie: 171/263 [65%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Kąt \alpha jest ostry oraz \tan\alpha=\frac{12}{5}.
Oblicz \sin\alpha.
Odpowiedź:
| \sin\alpha= | |
Podpunkt 10.2 (1 pkt)
Oblicz \cos\alpha.
Odpowiedź:
| \cos\alpha= | |
| Zadanie 11. 2 pkt ⋅ Numer: pp-20864 ⋅ Poprawnie: 94/201 [46%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
(2 pkt)
Kąt \alpha jest ostry i spełnia warunek
\tan\alpha=2.
Oblicz wartość wyrażenia \frac{6\sin\alpha+6\cos\alpha}{3\cos\alpha-3\sin\alpha}.
Odpowiedź:
| Wpisz odpowiedź: | |