Podgląd testu : lo2@sp-09-trygonom-1-pp-6
| Zadanie 1. 1 pkt ⋅ Numer: pp-10631 ⋅ Poprawnie: 374/652 [57%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wiadomo, że kąt \alpha jest ostry oraz
\sin\alpha=\frac{\sqrt{37}}{37}.
Oblicz wartość wyrażenia \sin \alpha-\cos\alpha.
Odpowiedź:
| \sin\alpha-\cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-10677 ⋅ Poprawnie: 78/124 [62%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W trójkącie prostokątnym przyprostokątne mają długości
3 i 9.
Oblicz sinus większego z kątów ostrych tego trójkąta.
Odpowiedź:
| \cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 1 pkt ⋅ Numer: pp-10662 ⋅ Poprawnie: 350/486 [72%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zapisz obwód trójkąta ABC w postaci p\cdot a:
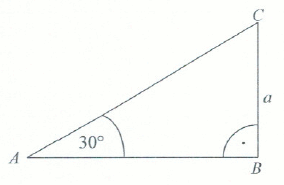

Podaj p.
Odpowiedź:
p=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10622 ⋅ Poprawnie: 339/558 [60%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Kąt \alpha należy do przedziału
(90^{\circ},180^{\circ}) i zachodzi równość
\cos\alpha=-\frac{1}{5}.
Oblicz \tan\alpha.
Odpowiedź:
\tan\alpha=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 5. 1 pkt ⋅ Numer: pp-11388 ⋅ Poprawnie: 215/458 [46%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Kąt \alpha jest kątem ostrym oraz
\sin\alpha+\cos\alpha=\frac{11}{10}.
Oblicz wartość wyrażenia (\sin\alpha-\cos\alpha)^2.
Odpowiedź:
| (\sin\alpha-\cos\alpha)^2= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20741 ⋅ Poprawnie: 92/251 [36%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Oblicz wartość wyrażenia
w=
(\tan{30^{\circ}}-\sin{45^{\circ}})(\cot{30^{\circ}}-\cos{60^{\circ}})
.
Odpowiedź:
| w= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pp-20255 ⋅ Poprawnie: 132/290 [45%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Kąt \beta jest ostry. Oblicz wartość wyrażenia
3+2\tan^2\beta.
Dane
\sin\beta=\frac{3}{8}=0.37500000000000
Odpowiedź:
| 3+2\tan^2\beta= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20288 ⋅ Poprawnie: 128/194 [65%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
W prostokątnym trójkącie ABC na przeciwprostokątnej
AB wybrano punkt D, a na
przyprostokątnej BC punkt
E w taki sposób, że
DE||AC oraz |BE|=|CE|=d.
Wyznacz tangens kąta EDC.
Dane
|AC|=12
d=6
d=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20265 ⋅ Poprawnie: 73/144 [50%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
» Oblicz \tan\alpha wiedząc, że
6\sin^2\alpha+14\cos^2\alpha=13 i
\alpha\in(0^{\circ},90^{\circ}).
Odpowiedź:
| \tan\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 10. 2 pkt ⋅ Numer: pp-20261 ⋅ Poprawnie: 46/99 [46%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
« Kąty \alpha i \beta są
kątami ostrymi w pewnym trójkącie prostokątnym oraz
\sin\alpha+\sin\beta=\frac{2\sqrt{10}}{5}.
Oblicz \sin\alpha\cdot \sin\beta.
Odpowiedź:
| \sin\alpha\cdot\sin\beta= | |
| Zadanie 11. 2 pkt ⋅ Numer: pp-20277 ⋅ Poprawnie: 57/94 [60%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
» Kąt ostry \alpha spełnia równanie
\sin\alpha+\cos\alpha=\frac{\sqrt{7}}{2}.
Oblicz (\sin\alpha-\cos\alpha)^2
Odpowiedź:
| (\sin\alpha-\cos\alpha)^2= | |
| Zadanie 12. 4 pkt ⋅ Numer: pp-30303 ⋅ Poprawnie: 54/248 [21%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
« Kąt \alpha jest rozwarty i spełnia warunek
\sin\alpha+\cos\alpha=\frac{1}{5}.
Oblicz \sin\alpha-\cos\alpha.
Odpowiedź:
| \sin\alpha-\cos\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 12.2 (2 pkt)
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | |