⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-10-funkcje-przeksz-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-10778 ⋅ Poprawnie: 649/848 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Dany jest wykres funkcji y=f(x).
Aby otrzymać wykres funkcji g(x)=f(x+6)-1 wykres funkcji f należy przesunąć o wektor o współrzędnych \vec{u}=[p, q].
Podaj współrzędne p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11752 ⋅ Poprawnie: 85/111 [76%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Wykres funkcji g(x)=\frac{1}{2}(x+5)^2-1
można otrzymać przesuwając wykres funkcji f(x)=\frac{1}{2}x^2
o wektor \vec{u}=[p,q].
Podaj współrzędne wektora p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10789 ⋅ Poprawnie: 737/1126 [65%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
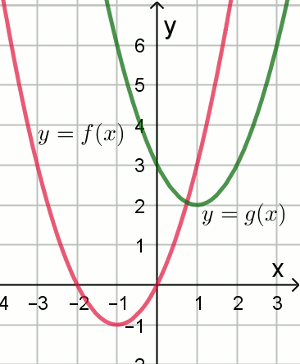
Funkcja g określona jest wzorem:
Odpowiedzi:
| A. g(x)=f(x-2)-3 | B. g(x)=f(x-2)+3 |
| C. g(x)=f(x+2)+3 | D. g(x)=f(x-3)+2 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10772 ⋅ Poprawnie: 350/495 [70%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
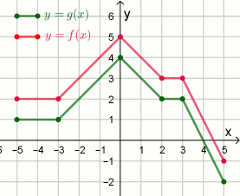
Funkcja f określona jest wzorem:
Odpowiedzi:
| A. f(x)=g(x-1) | B. f(x)=g(x)+1 |
| C. f(x)=g(x)-1 | D. f(x)=g(x+1) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10773 ⋅ Poprawnie: 363/520 [69%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
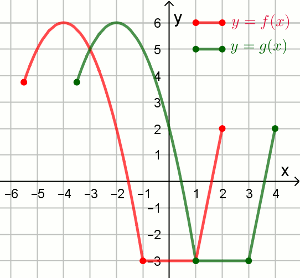
Funkcja f określona jest wzorem:
Odpowiedzi:
| A. f(x)=g(x+2) | B. f(x)=g(x)+2 |
| C. f(x)=g(x-2) | D. f(x)=g(x)-2 |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10777 ⋅ Poprawnie: 290/397 [73%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
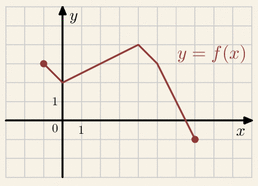
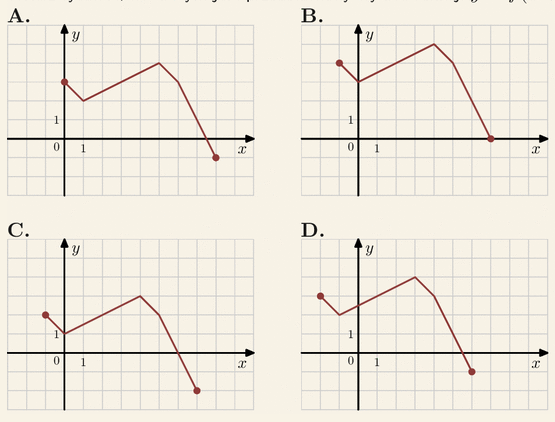
Na którym rysunku przedstawiony jest wykres funkcji y=f(x+1):
Odpowiedzi:
| A. D | B. C |
| C. A | D. B |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11571 ⋅ Poprawnie: 50/81 [61%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Wykres funkcji f(x)=x^2+3x-3 przesunięto
o wektor \vec{u}=[1,1] i otrzymano wykres funkcji
określonej wzorem g(x)=x^2+bx+c.
Podaj liczby b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11397 ⋅ Poprawnie: 295/523 [56%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=(-8,+\infty) oraz
ZW_f=\langle -1,8). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : ZW_g=(-8,1\rangle | T/N : ZW_g=\langle -8,1) |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10783 ⋅ Poprawnie: 409/519 [78%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Na rysunku 1. jest przedstawiony wykres funkcji f,
a na rysunku 2. – wykres funkcji g.
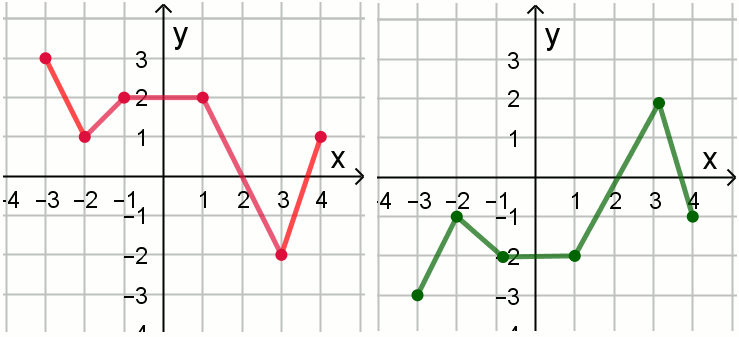
Funkcja g jest określona wzorem:
Odpowiedzi:
| A. g(x)=f(x)-4 | B. g(x)=-f(x) |
| C. g(x)=f(-x) | D. g(x)=f(x)+4 |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10786 ⋅ Poprawnie: 157/277 [56%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Na rysunku 1. przedstawiono wykres funkcji
y=f(x) (czerwony), a na rysunku 2.
wykres funkcji y=g(x) (zielony):
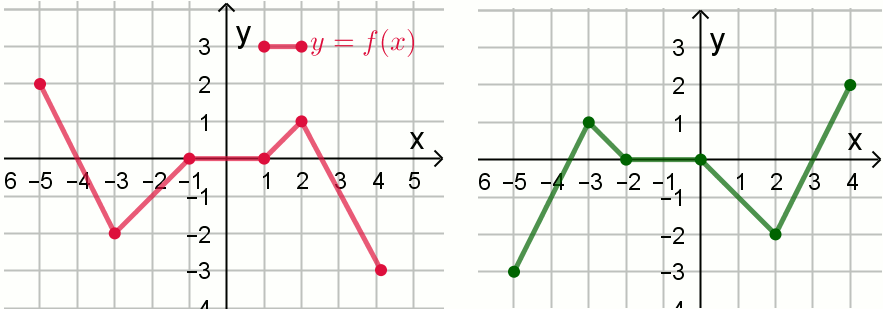
Funkcja f określona jest wzorem:
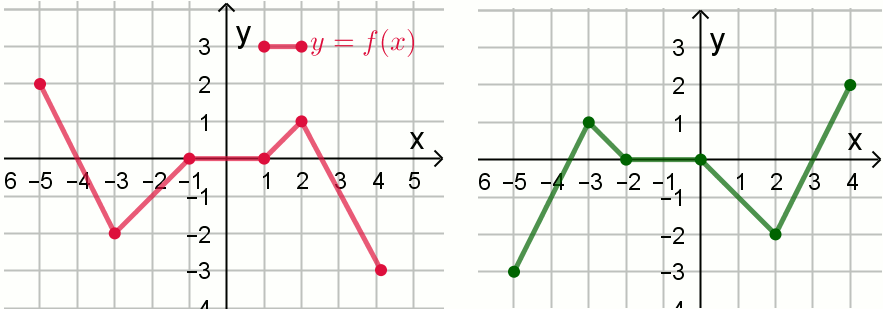
Odpowiedzi:
| A. f(x)=g(x-1) | B. f(x)=g(x+1) |
| C. f(x)=g(-x-1) | D. f(x)=g(-x)-1 |
| Zadanie 11. 1 pkt ⋅ Numer: pp-10768 ⋅ Poprawnie: 204/319 [63%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
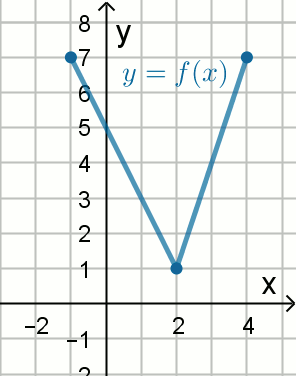
Funkcja, której wykres jest symetryczny do tego wykresu względem osi Oy określona jest wzorem:
Odpowiedzi:
| A. y=f(-x)+1 | B. y=-f(x) |
| C. g(x)=f(-x) | D. y=f(x)+1 |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10781 ⋅ Poprawnie: 193/257 [75%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
« Funkcja f ma n=5 miejsc zerowych.
Ile miejsc zerowych ma funkcja określona wzorem g(x)=-f(x-9)?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. 1 pkt ⋅ Numer: pp-11395 ⋅ Poprawnie: 302/494 [61%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=-5x^2-x przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=ax^2+bx.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11748 ⋅ Poprawnie: 40/47 [85%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=-5\sqrt{x}-1 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=a\sqrt{x}+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11400 ⋅ Poprawnie: 183/463 [39%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Wykres funkcji g jest symetryczny do wykresu
funkcji f określonej wzorem
f(x)=\frac{-1}{-x-4}
względem początku układu współrzędnych.
Zapisz wzór funkcji g w postaci
g(x)=\frac{a}{x+b}.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |