Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pp-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-11595 ⋅ Poprawnie: 119/162 [73%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Do wykresu funkcji kwadratowej określonej wzorem y=ax^2
należy punkt o współrzędnych (-2\sqrt{2},56\sqrt{3}).
Wyznacz współczynnik a.
Odpowiedź:
a=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10979 ⋅ Poprawnie: 173/317 [54%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dana jest funkcja f określona wzorem f(x)=-5(x-2)^2+4.
Wyznacz największą wartość funkcji określonej wzorem h(x)=f(x-5)+5.
Odpowiedź:
h_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11006 ⋅ Poprawnie: 345/643 [53%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wskaż funkcję, która w przedziale
(-\infty,6) jest malejąca:
Odpowiedzi:
| A. y=-(x+6)^2+6 | B. y=(x-6)^2+7 |
| C. y=-(x-6)^2-7 | D. y=(x+7)^2+6 |
| E. y=(x+6)^2+7 | F. y=(x-7)^2+6 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11040 ⋅ Poprawnie: 241/405 [59%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Punkt P=(9,10) należy do wykresu funkcji
g(x)=x^2-mx+1.
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11084 ⋅ Poprawnie: 115/172 [66%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dana jest funkcja y=x^2-6.
Do zbioru ZW_f nie należy liczba:
Odpowiedzi:
| A. 2-3\sqrt{3} | B. 8-5\sqrt{7} |
| C. 2-4\sqrt{6} | D. 4-6\sqrt{2} |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11041 ⋅ Poprawnie: 367/696 [52%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Wyznacz największa wartość funkcji określonej wzorem
y=-3(x-4)(x-6).
Odpowiedź:
| y_{max}= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11075 ⋅ Poprawnie: 99/170 [58%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Dana jest funkcja kwadratowa określona wzorem f(x)=(4-x)(3x+6).
Wierzchołek wykresu tej funkcji należy do prostej określonej równaniem x=m.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11020 ⋅ Poprawnie: 57/112 [50%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
«« Funkcja kwadratowa spełnia warunki: y=px^2+qx+r i
p\cdot r \lessdot 0.
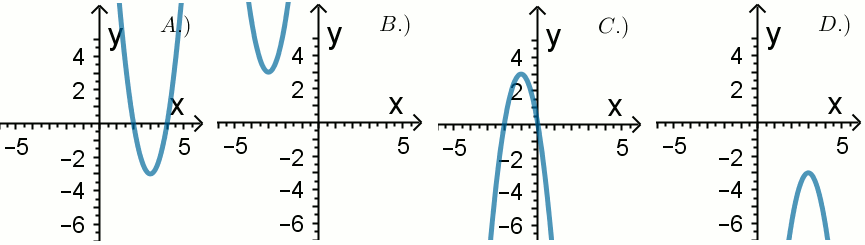

Wykres tej funkcji pokazano na rysunku:
Odpowiedzi:
| A. A | B. D |
| C. B | D. C |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11728 ⋅ Poprawnie: 4/13 [30%] | Rozwiąż |
Podpunkt 9.1 (0.2 pkt)
Zbiorem wartości funkcji y=-(x-10)(x+10)
określonej dla x\in(2,5\rangle jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. \langle p,q) | B. (p,q\rangle |
| C. \langle p,q\rangle | D. (-\infty,p\rangle |
| E. (p,q) | F. (p,+\infty) |
Podpunkt 9.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 10. 1 pkt ⋅ Numer: pp-11081 ⋅ Poprawnie: 41/75 [54%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
» Wykres funkcji kwadratowej opisanej wzorem g(x)=-x^2-6x+4
przecięto prostą o równaniu y=9. Niech
P i Q będą punktami
przecięcia tych wykresów.
Oblicz |PQ|.
Odpowiedź:
|PQ|=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pp-11466 ⋅ Poprawnie: 204/339 [60%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Dana jest funkcja kwadratowa
f(x)=-0,5(x+3m)^2+12m, gdzie
m > 0.
Wówczas:
Odpowiedzi:
| A. największą wartością funkcji jest -12m | B. dla m=-\frac{1}{2} funkcja jest rosnąca |
| C. dla pewnego m funkcja ma jedno miejsce zerowe | D. wierzchołek paraboli, która jest wykresem tej funkcji należy do prostej y=-4x |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11730 ⋅ Poprawnie: 27/45 [60%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Większa część zawodników klubu sportowego liczącego 81 osób,
zachorowała na grypę. Każdy zdrowy zawodnik postanowił wysłać każdemu choremu kartkę z
pozdrowieniami. Liczba wszystkich wysłanych kartek była największa możliwa.
Ilu zawodników było chorych?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 13. 1 pkt ⋅ Numer: pp-11058 ⋅ Poprawnie: 93/186 [50%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
« Wierzchołek paraboli będącej wykresem funkcji kwadratowej określonej wzorem
y=(2x+7)^2+\frac{27}{2} należy do prostej o równaniu
y=......\cdot x.
Podaj brakującą liczbę.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 14. 1 pkt ⋅ Numer: pp-10971 ⋅ Poprawnie: 132/197 [67%] | Rozwiąż |
Podpunkt 14.1 (0.2 pkt)
Równanie x^2-(k-5)x+49=0 z niewiadomą
x ma dwa różne rozwiązania wtedy i tylko wtedy, gdy parametr
k należy do zbioru A. Zapisz zbiór
Aw postaci sumy przedziałów.
Zbiór A jest postaci:
Odpowiedzi:
| A. \langle p,q\rangle | B. (-\infty,p) |
| C. (-\infty,p)\cap(q,+\infty) | D. (-\infty,p)\cup(q,+\infty) |
| E. (p,+\infty) | F. (p,q) |
Podpunkt 14.2 (0.8 pkt)
Liczba p jest najmniejszym, a liczba q
największym z końców liczbowych tych przedziałów.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 15. 1 pkt ⋅ Numer: pp-10962 ⋅ Poprawnie: 385/588 [65%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Iloczyn (x-7)(8-x) jest nieujemny, wtedy i tylko wtedy, gdy liczba x
należy do zbioru A. Zapisz zbiór A
w postaci sumy przedziałów.
Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |