Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10989 ⋅ Poprawnie: 706/1015 [69%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Największą wartością funkcji kwadratowej
f(x)=-4(x+5)^2-8 jest ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10996 ⋅ Poprawnie: 345/564 [61%] | Rozwiąż |
Podpunkt 2.1 (0.2 pkt)
Zbiór tych wszystkich wartości m, dla których funkcja kwadratowa
określona wzorem f(x)=x^2+7x+m nie ma ani
jednego miejsca zerowego jest przedziałem liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (-\infty, p) | B. (p, +\infty) |
| C. (-\infty, p\rangle | D. \langle p, q\rangle |
| E. \langle p, +\infty) | F. (p, q) |
Podpunkt 2.2 (0.8 pkt)
Podaj najmniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11023 ⋅ Poprawnie: 295/454 [64%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
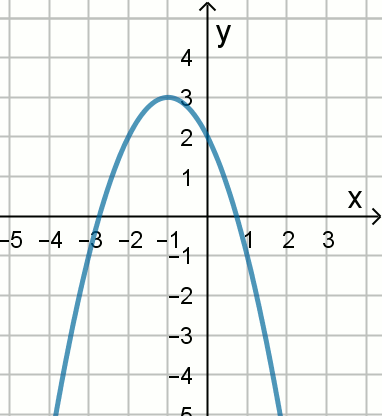
Na podstawie wykresu funkcji określonej wzorem
y=ax^2+bx+c wskaż jej wzór:

Odpowiedzi:
| A. y=-x^2-2x+2 | B. y=-x^2+2x+2 |
| C. y=x^2-2x+4 | D. y=x^2+2x+4 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10978 ⋅ Poprawnie: 475/746 [63%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Najmniejszą wartość w przedziale
\langle 6, 10\rangle funkcja kwadratowa
określona wzorem
f(x)=-\left(x-9\right)^{2}+5
przyjmuje dla argumentu ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10972 ⋅ Poprawnie: 713/884 [80%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wiadomo, że 36x^2-12x+1=0.
Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20339 ⋅ Poprawnie: 76/172 [44%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Najmniejszą wartość równą -2 trójmian
y=x^2+bx+c osiąga dla x=1.
Oblicz b.
Odpowiedź:
| b= | |
Podpunkt 6.2 (1 pkt)
Oblicz c.
Odpowiedź:
| c= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20360 ⋅ Poprawnie: 21/52 [40%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
» Wyznacz najmniejszą wartość funkcji
f(x)=bx+ax^2.
Dane
a=\frac{2}{3}=0.66666666666667
b=-\frac{3}{2}=-1.50000000000000
b=-\frac{3}{2}=-1.50000000000000
Odpowiedź:
| min= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20382 ⋅ Poprawnie: 16/59 [27%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
» Iloczyn dwóch liczb ujemnych jest równy 3256,
a jedna z nich jest o 7 mniejsza od połowy
drugiej liczby.
Podaj większą z tych liczb.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pr-20982 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Rozwiąż równanie
\sqrt{3x+25}-\sqrt{x+7}=2
.
Podaj najmniejsze z rozwiązań tego równania.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
Podaj największe z rozwiązań tego równania.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 10. 4 pkt ⋅ Numer: pr-30041 ⋅ Poprawnie: 12/17 [70%] | Rozwiąż |
Podpunkt 10.1 (3 pkt)
« Wyznacz te wartości parametru m, dla których
równanie x^2+(m-a)x+m-2-a=0 ma dwa różne pierwiastki
rzeczywiste takie, że ich suma kwadratów jest minimalna możliwa.
Podaj najmniejsze możliwe m, które spełnia warunki zadania.
Dane
a=5
Odpowiedź:
m_{min}=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
Ile rozwiązań ma to zadanie?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)