Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-11643 ⋅ Poprawnie: 95/193 [49%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Do wykresu funkcji kwadratowej określonej wzorem y=x^2+bx+c
należą punkty o współrzędnych (-1,14) i
(-8,-7).
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11078 ⋅ Poprawnie: 196/346 [56%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dana jest funkcja f(x)=-2(x-9)(x-12).
Wyznacz maksymalny przedział, w którym funkcja f jest
rosnąca.
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11024 ⋅ Poprawnie: 121/339 [35%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku pokazano tylko część wykresu funkcji
f(x)=ax^2+bx+c, dla której
D_f=\mathbb{R}.
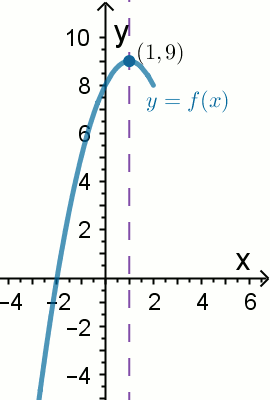

Wówczas:
Odpowiedzi:
| T/N : funkcja przyjmuje wartości większe od zera dla x \lessdot 1 | T/N : f(-5)=h(8) |
| T/N : zbiorem wartości tej funkcji jest przedział (-\infty,9) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11466 ⋅ Poprawnie: 204/339 [60%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Dana jest funkcja kwadratowa
f(x)=-0,5(x+2m)^2+10m, gdzie
m > 0.
Wówczas:
Odpowiedzi:
| A. największą wartością funkcji jest -10m | B. wierzchołek paraboli, która jest wykresem tej funkcji należy do prostej y=-5x |
| C. dla pewnego m funkcja ma jedno miejsce zerowe | D. dla m=-\frac{1}{2} funkcja jest rosnąca |
| Zadanie 5. 1 pkt ⋅ Numer: pr-10110 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (0.2 pkt)
Zapisz dziedzinę funkcji określonej wzorem
f(x)=
\sqrt{\frac{x^3}{x^2+x-42}}
-
\frac{x\sqrt{x}}{\sqrt{x^2+x-42}}
w postaci sumy przedziałów.
Suma ta ma postać:
Odpowiedzi:
| A. (-\infty,p\rangle\cup\langle q, +\infty) | B. \langle p,+\infty) |
| C. (p,+\infty) | D. (p,q) |
| E. \langle p,q\rangle | F. (-\infty,p) |
Podpunkt 5.2 (0.8 pkt)
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20930 ⋅ Poprawnie: 35/62 [56%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=a(x-p)^2+q dla argumentu
7 osiąga wartość największą równą
10. Wiedząc, że do jej wykresu należy punkt
należy punkt A=(5,7), wyznacz wzór tej funkcji.
Podaj współczynnik a.
Odpowiedź:
| a= | |
Podpunkt 6.2 (1 pkt)
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20941 ⋅ Poprawnie: 130/224 [58%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Wiadomo, że x-y=24, a także, że suma x^2+y^2
jest najmniejsza możliwa.
Podaj liczbę x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Podaj liczbę y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20991 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Liczby 3-2\sqrt{3} i 3+2\sqrt{3}
są miejscami zerowymi funkcji określonej wzorem
f(x)=x^2+(p+q)x+p^2-q^2.
Wyznacz liczbę p.
Odpowiedź:
| p= | |
Podpunkt 8.2 (1 pkt)
Wyznacz liczbę q.
Odpowiedź:
| q= | |
| Zadanie 9. 2 pkt ⋅ Numer: pr-20093 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
«« Wyznacz te wartości parametru m\in\mathbb{R},
dla których równanie (m+5)x^2-(m+7)x+3=0 ma
dokładnie jedno rozwiązanie.
Podaj największe możliwe m spełniające warunki zadania.
Odpowiedź:
m_{max}=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
Podpunkt 9.2 (1 pkt)
Podaj sumę wszystkich wyznaczonych wartości parametru
m.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 10. 4 pkt ⋅ Numer: pr-30839 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 10.1 (2 pkt)
Rozwiąż równanie
\sqrt{-2+x-4\sqrt{x-6}}+\sqrt{3+x-6\sqrt{x-6}}=1
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (2 pkt)
Podaj największy z końców
liczbowych tych przedziałów.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 11. 4 pkt ⋅ Numer: pr-30089 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
Dla jakich wartości parametru m\in\mathbb{R} równanie
2x^2-(m+2-a)|x|+m-a=0
ma dwa różne rozwiązania?
Podaj największe możliwe m.
Dane
a=-4
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (2 pkt)
Dla ilu całkowitych wartości
m\in\langle -10,10 \rangle warunki zadania są
spełnione?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)