⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-10547 ⋅ Poprawnie: 663/914 [72%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\beta=116^{\circ} i
\gamma=23^{\circ}:
Obicz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10548 ⋅ Poprawnie: 276/537 [51%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\alpha=52^{\circ}:
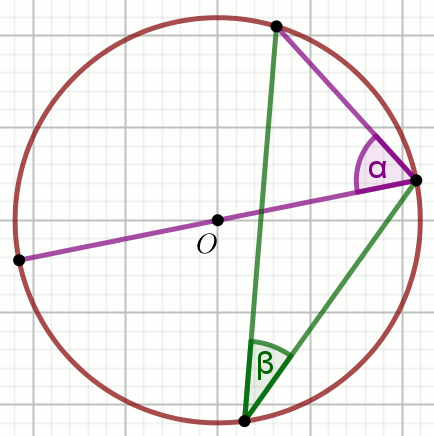
Oblicz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10492 ⋅ Poprawnie: 123/173 [71%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym:
|AO|=7 oraz |AB|=7\sqrt{3}:
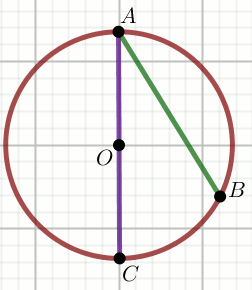
Wówczas:
Odpowiedzi:
| A. |\sphericalangle BOC|=60^{\circ} | B. |\sphericalangle BCA|=45^{\circ} |
| C. |\sphericalangle BCA|=90^{\circ} | D. |\sphericalangle BAC|=45^{\circ} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10536 ⋅ Poprawnie: 110/152 [72%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Punkt O jest środkiem okręgu, przy czym \beta=34^{\circ}:
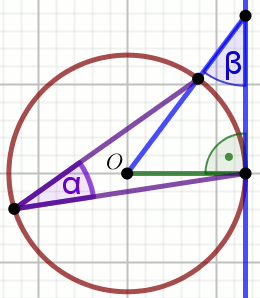
Kąt \alpha, zaznaczony na rysunku, ma miarę:
Odpowiedzi:
| A. 26^{\circ} | B. 23^{\circ} |
| C. 32^{\circ} | D. 31^{\circ} |
| E. 24^{\circ} | F. 28^{\circ} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10509 ⋅ Poprawnie: 39/61 [63%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
«« Kąt wpisany w okrąg o promieniu długości 48 ma miarę
75^{\circ}. Kąt ten oparty jest na łuku o długości k\cdot \pi.
Wyznacz liczbę k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 6. 1 pkt ⋅ Numer: pp-10518 ⋅ Poprawnie: 187/269 [69%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Punkt O jest środkiem okręgu,
kąt \alpha ma miarę 248^{\circ}
a prosta jest styczna do tego okręgu:
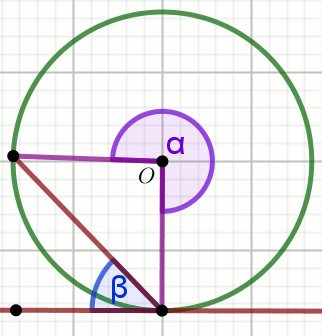
Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 7. 1 pkt ⋅ Numer: pp-10524 ⋅ Poprawnie: 148/203 [72%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Prosta jest styczną do okręgu, a kąty \alpha i
\beta mają miary:
\alpha=34^{\circ} oraz
\beta=25^{\circ}:
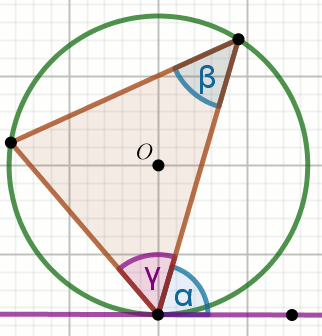
Wyznacz miarę stopniową kąta \gamma.
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-11513 ⋅ Poprawnie: 456/830 [54%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
(1 pkt)
Punkt O jest środkiem okręgu na rysunku, a kąt
\alpha ma miarę 29^{\circ}:
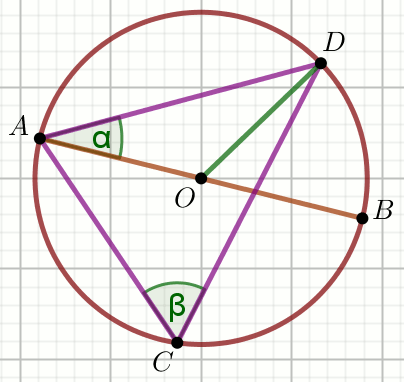
Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 1 pkt ⋅ Numer: pp-11653 ⋅ Poprawnie: 14/33 [42%] | Rozwiąż |
Podpunkt 9.1 (0.5 pkt)
« Okręgi o_1(A, 2) oraz o_2(B,2m-1)
są styczne wewnętrznie, a odległość ich środków jest równa 22.
Wyznacz najmniejszą wartość parametru m.
Odpowiedź:
| m_{min}= | |
Podpunkt 9.2 (0.5 pkt)
Wyznacz największą wartość parametru m.
Odpowiedź:
| m_{max}= | |
| Zadanie 10. 1 pkt ⋅ Numer: pp-11738 ⋅ Poprawnie: 34/52 [65%] | Rozwiąż |
Podpunkt 10.1 (0.5 pkt)
Okręgi o_1(A, r_1) oraz o_2(B,r_2)
(r_1\lessdot r_2) są styczne wewnętrznie, a odległość ich środków jest równa \frac{13}{6}.
Stosunek długości promieni tych okręgów jest równy 2.
Oblicz r_1.
Odpowiedź:
| r_1= | |
Podpunkt 10.2 (0.5 pkt)
Oblicz r_2.
Odpowiedź:
| r_2= | |
| Zadanie 11. 1 pkt ⋅ Numer: pp-10476 ⋅ Poprawnie: 420/638 [65%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Dane są okręgi, w których |O_1A|=20,
|O_2B|=12 i
|O_1O_2|=64:
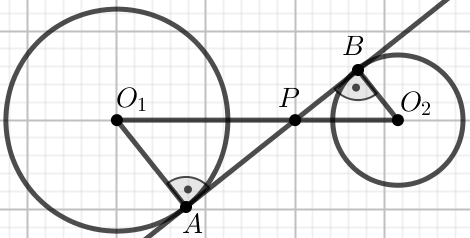
Oblicz długość odcinka O_1P.
Odpowiedź:
|O_1P|=
(wpisz liczbę całkowitą)
| Zadanie 12. 1 pkt ⋅ Numer: pp-10562 ⋅ Poprawnie: 332/471 [70%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Okręgi o_1(O_1, 3) i
o_2(O_2,5) są styczne zewnętrznie w punkcie
S, a prosta O_1P
jest styczną do okręgu o_2:
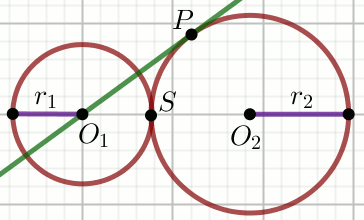
Oblicz pole powierzchni trójkąta O_1O_2P.
Odpowiedź:
| P_{\triangle O_1O_2P}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 13. 1 pkt ⋅ Numer: pp-11648 ⋅ Poprawnie: 90/142 [63%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Odcinek AB ma długość 8
i jest cięciwą okręgu o promieniu \frac{17}{2}.
Oblicz odległość d cięciwy AB od środka tego okręgu.
Odpowiedź:
| d= | |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11651 ⋅ Poprawnie: 19/26 [73%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Dwa promienie okręgu tworzą kąt środkowy tego okręgu o mierze 16^{\circ}.
Przez końce tych promieni położone na okręgu poprowadzono styczne do tego okręgu, które
przecięły się w punkcie P.
Wyznacz miarę stopniową kąta, pod którym widać ten okrąg z punktu P.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)