Podgląd testu : lo2@sp-13-okr-i-kola-pp-6
| Zadanie 1. 1 pkt ⋅ Numer: pp-10548 ⋅ Poprawnie: 276/537 [51%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\alpha=68^{\circ}:
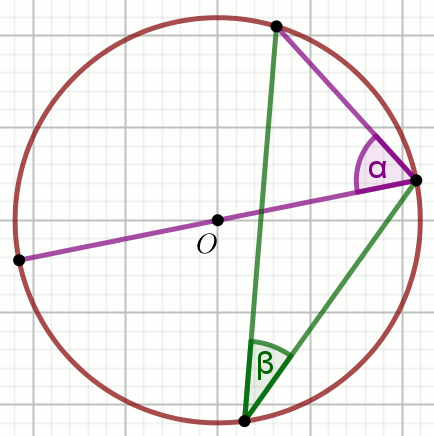

Oblicz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10509 ⋅ Poprawnie: 39/61 [63%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
«« Kąt wpisany w okrąg o promieniu długości 48 ma miarę
75^{\circ}. Kąt ten oparty jest na łuku o długości k\cdot \pi.
Wyznacz liczbę k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10567 ⋅ Poprawnie: 274/452 [60%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Okręgi o_1(A, 4) i
o_2(B, 14) przecinają się w dwóch punktach:
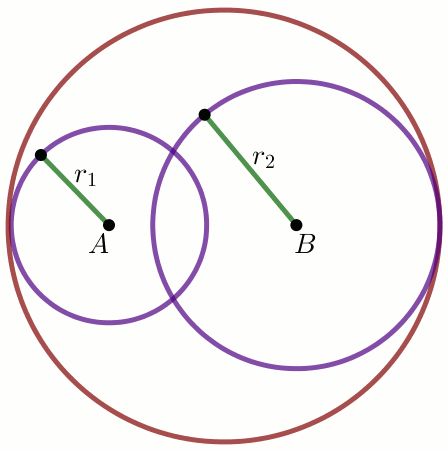

Do odcinka AB należy środek okręgu o_3(C, r_3) stycznego wewnętrznie do obu okręgów o_1 i o_2.
Oblicz długość promienia r_3 wiedząc, że |AB|=16.
Odpowiedź:
r_3=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-11650 ⋅ Poprawnie: 32/55 [58%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Jaką część okręgu o promieniu 10
stanowi jego łuk o długości 9\pi?
Odpowiedź:
| \frac{m}{n}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 2 pkt ⋅ Numer: pp-20950 ⋅ Poprawnie: 7/24 [29%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
W trójkąt równoramienny o podstawie |AB|=5
i ramionach |AC|=|BC|=6 wpisano okrąg, który jest styczny
do boków BC i AC odpowiednio w punktach
E i F.
Oblicz stosunek |AF|:|FC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20202 ⋅ Poprawnie: 73/149 [48%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Na trójkącie ABC opisano okrąg.
Z punktu P leżącego poza okręgiem poprowadzono
styczną do okręgu w punkcie A oraz sieczną,
która przecięła okrąg w punktach B i
C.
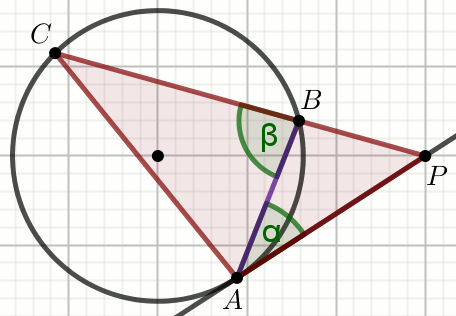
Oblicz miary kątów trójkąta APC.

Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=58^{\circ}
\beta=89^{\circ}
\beta=89^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Podaj miarę stopniową największego z kątów tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20224 ⋅ Poprawnie: 87/161 [54%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Na trójkątach równobocznych ACD i
BEC, których podstawy zawierają się w jednej
prostej, opisano dwa okręgi jak na rysunku. Okręgi te przecięły się w punktach
C i P.
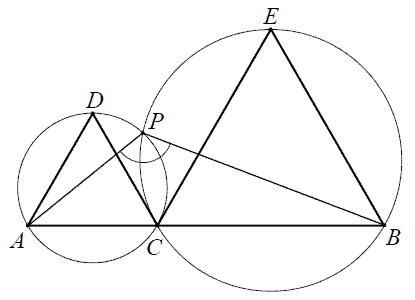

Oblicz miarę stopniową kąta APB.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 4 pkt ⋅ Numer: pp-30017 ⋅ Poprawnie: 20/89 [22%] | Rozwiąż |
Podpunkt 8.1 (4 pkt)
» W kwadrat o boku długości a\sqrt{2} wpisano
cztery okręgi jak na rysunku. Następnie narysowano koło zawarte w kwadracie i
styczne do tych czterech okręgów.
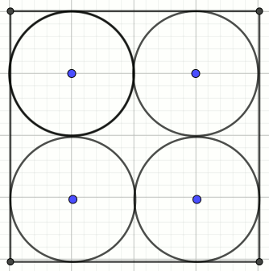

Oblicz promień tego koła.
Dane
a=18
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 4 pkt ⋅ Numer: pp-30395 ⋅ Poprawnie: 68/153 [44%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
«« Punkt O jest środkiem okręgu:


Oblicz |AC|.
Dane
|AB|=10
|BN|=6
|CN|=3
|BN|=6
|CN|=3
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 9.2 (2 pkt)
Oblicz |MC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)