⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10505 ⋅ Poprawnie: 178/231 [77%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O na rysunku jest środkiem okręgu, przy czym
\alpha=64^{\circ}:
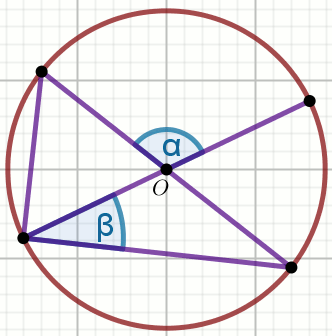
Wyznacz miarę zaznaczonego na rysunku kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10508 ⋅ Poprawnie: 61/107 [57%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Kąt \alpha wpisany w okrąg o promieniu długości 18
oparty jest na łuku o długości 6\pi.
Wyznacz miarę tego kąta.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10566 ⋅ Poprawnie: 192/310 [61%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Okręgi o_1(O_1, 2) i
o_2(O_2, 8) są styczne zewnętrznie w punkcie
S, a prosta k
jest styczną do tych okręgów:
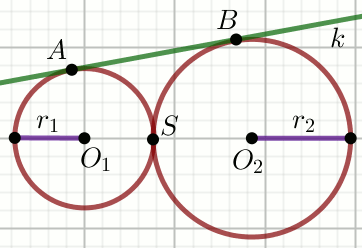
Oblicz długość odcinka AB.
Odpowiedź:
|AB|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 4. 1 pkt ⋅ Numer: pp-11651 ⋅ Poprawnie: 19/26 [73%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Dwa promienie okręgu tworzą kąt środkowy tego okręgu o mierze 110^{\circ}.
Przez końce tych promieni położone na okręgu poprowadzono styczne do tego okręgu, które
przecięły się w punkcie P.
Wyznacz miarę stopniową kąta, pod którym widać ten okrąg z punktu P.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 2 pkt ⋅ Numer: pp-20949 ⋅ Poprawnie: 37/43 [86%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Cięciwa CD okręgu o środku O
jest prostopadła do średnicy AB tego okręgu i przecina ją w punkcie
P takim, że |AP|:|PB|=169:1
oraz |OP|=84.
Oblicz długość promienia tego okręgu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (1 pkt)
Oblicz długość cięciwy CD.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20893 ⋅ Poprawnie: 98/172 [56%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
«« Dany jest okrąg:
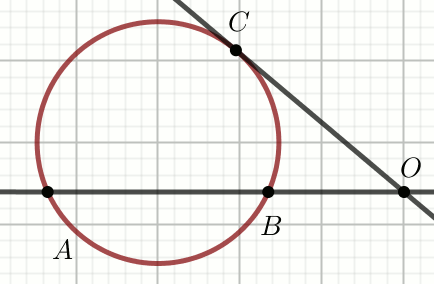
Oblicz długość cięciwy |AB|.
Dane
|BO|=18
|CO|=24
|CO|=24
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 4 pkt ⋅ Numer: pp-30017 ⋅ Poprawnie: 20/89 [22%] | Rozwiąż |
Podpunkt 7.1 (4 pkt)
» W kwadrat o boku długości a\sqrt{2} wpisano
cztery okręgi jak na rysunku. Następnie narysowano koło zawarte w kwadracie i
styczne do tych czterech okręgów.
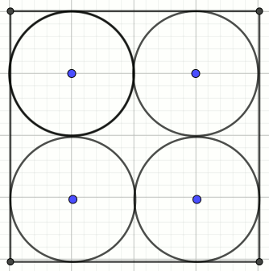
Oblicz promień tego koła.
Dane
a=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 4 pkt ⋅ Numer: pp-30395 ⋅ Poprawnie: 68/153 [44%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
«« Punkt O jest środkiem okręgu:
Oblicz |AC|.
Dane
|AB|=29
|BN|=20
|CN|=10
|BN|=20
|CN|=10
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
Oblicz |MC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)