⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pr-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-10504 ⋅ Poprawnie: 722/1039 [69%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu, w którym
\alpha=40^{\circ}:
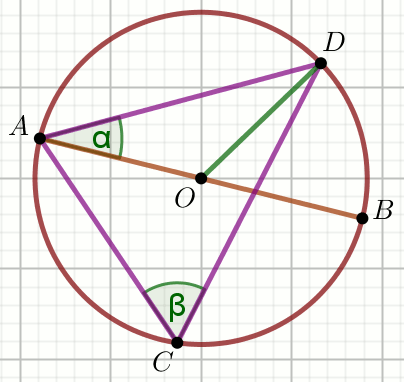
Oblicz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10525 ⋅ Poprawnie: 67/116 [57%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt O jest środkiem okręgu, przy czym
\alpha=150^{\circ}:
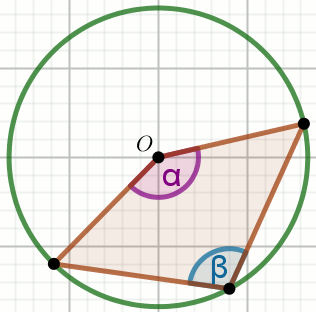
Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10569 ⋅ Poprawnie: 300/394 [76%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Dane są okręgi o_1\left(A, 8\right) i
o_2\left(B, \frac{19}{2}\right), przy czym
|AB|=\frac{13}{2}.
Okręgi te:
Odpowiedzi:
| A. są rozłączne wewnętrznie | B. są styczne wewnętrznie |
| C. mają dwa punkty wspólne | D. są rozłączne zewnętrznie |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11740 ⋅ Poprawnie: 9/17 [52%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Jaką część okręgu o promieniu 5\pi
stanowi jego łuk o długości 9\pi^2?
Odpowiedź:
| \frac{m}{n}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 2 pkt ⋅ Numer: pp-20952 ⋅ Poprawnie: 6/36 [16%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
« Końce A i B średnicy okręgu
są odległe od stycznej do tego okręgu odpowiednio o
36 i 58.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| r= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20231 ⋅ Poprawnie: 116/163 [71%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Dane są dwa okręgi o środkach w punktach P
i R, styczne zewnętrznie w punkcie
C.
Prosta AB jest styczna do obu okręgów odpowiednio
w punktach A i B oraz
|\sphericalangle ABC|=\beta:
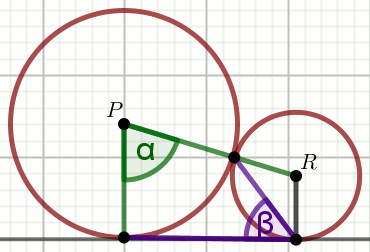
Oblicz miarę kąta \alpha. Wynik zapisz w stopniach bez jednostki.
Dane
\beta=76^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 4 pkt ⋅ Numer: pp-30019 ⋅ Poprawnie: 14/42 [33%] | Rozwiąż |
Podpunkt 7.1 (4 pkt)
« Okręgi o_1 i o_2
o środkach odpowiednio A i
B i promieniach odpowiednio
r_1 i r_2 są styczne
wewnętrznie. Z punktu A poprowadzono półproste
styczne do okręgu o_2 w punktach
M i N.
Oblicz pole czworokąta AMBN.
Dane
r_1=26
r_2=7
r_2=7
Odpowiedź:
P_{AMBN}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 8. 4 pkt ⋅ Numer: pp-30395 ⋅ Poprawnie: 68/153 [44%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
«« Punkt O jest środkiem okręgu:
Oblicz |AC|.
Dane
|AB|=73
|BN|=48
|CN|=24
|BN|=48
|CN|=24
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
Oblicz |MC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)