Podgląd testu : lo2@sp-16-trojkaty-pole-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10591 ⋅ Poprawnie: 305/384 [79%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Trójkąt ABC jest podobny do trójkąta
A_1B_1C_1 w skali
k=\frac{11}{8}. Stosunek pola trójkąta
ABC do pola trójkąta A_1B_1C_1
jest równy:
Odpowiedź:
| \frac{P_{\triangle ABC}}{P_{\triangle A_1B_1C_1}}= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11598 ⋅ Poprawnie: 48/118 [40%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Promień koła ma długość 5, a kąt wycinka tego koła ma miarę
195^{\circ}. Oblicz pole powierzchni tego wycinka i zapisz wynik w postaci
p\cdot\pi.
Podaj liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10647 ⋅ Poprawnie: 380/532 [71%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
W trójkącie równoramiennym ramię o długości
10\sqrt{3} tworzy z podstawą kąt o mierze
67,5^{\circ}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-10654 ⋅ Poprawnie: 235/356 [66%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Oblicz pole powierzchni równoległoboku o bokach długości \frac{7}{10} i
9 oraz kącie ostrym o mierze
45^{\circ}.
Odpowiedź:
| P= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 1 pkt ⋅ Numer: pp-10679 ⋅ Poprawnie: 172/233 [73%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Pole powierzchni rombu o obwodzie długości 80 jest równe
100. Kąt ostry tego rombu ma miarę
\alpha.
Wówczas:
Odpowiedzi:
| A. 14^{\circ} \lessdot \alpha \lessdot 15^{\circ} | B. 75^{\circ} \lessdot \alpha \lessdot 76^{\circ} |
| C. 29^{\circ} \lessdot \alpha \lessdot 30^{\circ} | D. 60^{\circ} \lessdot \alpha \lessdot 61^{\circ} |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20279 ⋅ Poprawnie: 104/190 [54%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Dwa boki trójkąta mają długości \frac{4}{5} i
\frac{3}{5}, a pole powierzchni tego trójkąta jest równe
\frac{4}{25}.
Wyznacz z dokładnością do jednego stopnia miarę kąta zawartego między tymi bokami.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-21028 ⋅ Poprawnie: 23/40 [57%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Pole powierzchni trójkąta jest równe 84, a promień
okręgu wpisanego w ten trójkąt ma długość 4.
Wiedząc, że długości boków tego trójkąta są kolejnymi liczbami naturalnymi, oblicz długość najdłuższej wysokości tego trójkąta.
Odpowiedź:
| h_{min}= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20912 ⋅ Poprawnie: 21/34 [61%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
W trójkącie ostrokątnym równoramiennym ABC, |AC|=|BC|,
poprowadzono wysokości CD i BE. Stosunek pól powierzchni
trójkątów ABE i ADC jest równy
P_{ABE}:P_{ADC}=\frac{256}{289}, a obwód tego trójkąta ma długość
100.
Oblicz pole powierzchni trójkąta ABC.
Odpowiedź:
P_{\triangle ABC}=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20918 ⋅ Poprawnie: 2/4 [50%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Dwa koła mają promień o długości 6 i są tak położone, że do okręgu każdego z nich
należy środek drugiego z kół:
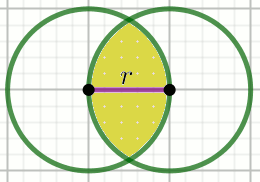

Oblicz pole obszaru wspólnego tych kół.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20887 ⋅ Poprawnie: 58/165 [35%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
» Oblicz długość promienia okręgu na rysunku wiedząc, że
|AC|-|AB|=30\sqrt{2} oraz
|BC|=50:
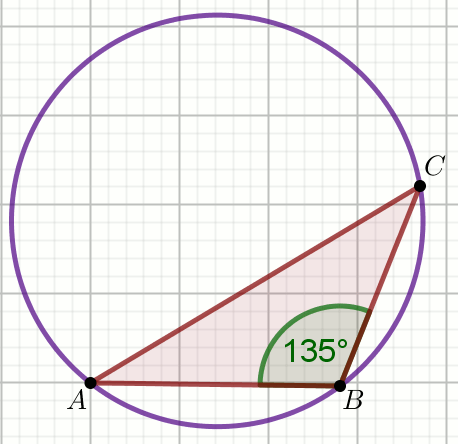

Odpowiedź:
R=
(wpisz liczbę całkowitą)