Podgląd testu : lo2@sp-16-trojkaty-pole-pr-3
Zadanie 1. 1 pkt ⋅ Numer: pp-10515 ⋅ Poprawnie: 92/170 [54%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
25:49 , mogą być równe:
Odpowiedzi:
A. 10:\frac{75}{7}
B. 7:\frac{25}{7}
C. 5:\frac{49}{5}
D. 5:\frac{25}{7}
Zadanie 2. 1 pkt ⋅ Numer: pp-11602 ⋅ Poprawnie: 5/11 [45%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
W trójkącie prostokątnym stosunek długości przyprostokątnej do długości przeciwprostokątnej jest równy
8:17 .
Oblicz stosunek pola powierzchni koła wpisanego w ten trójkąt do pola powierzchni koła opisanego
na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 3. 1 pkt ⋅ Numer: pp-10669 ⋅ Poprawnie: 411/603 [68%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
Dany jest trójkąt
ABC , w którym
|AB|=7 ,
|BC|=10
oraz
\sin\sphericalangle ABC=\frac{\sqrt{51}}{10} .
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
Zadanie 4. 1 pkt ⋅ Numer: pp-10654 ⋅ Poprawnie: 235/356 [66%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
Oblicz pole powierzchni równoległoboku o bokach długości
\frac{4}{7} i
10 oraz kącie ostrym o mierze
45^{\circ} .
Odpowiedź:
Zadanie 5. 1 pkt ⋅ Numer: pp-11512 ⋅ Poprawnie: 483/859 [56%]
Rozwiąż
Podpunkt 5.1 (1 pkt)
Oblicz pole powierzchni prostokąta,którego przekątne mają długość
2 i
przecinają się pod kątem o mierze
60^{\circ} .
Odpowiedź:
Zadanie 6. 2 pkt ⋅ Numer: pp-20745 ⋅ Poprawnie: 43/196 [21%]
Rozwiąż
Podpunkt 6.1 (2 pkt)
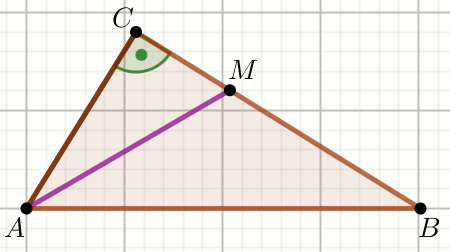
» Odcinki
AM i
MB
na rysunku maja równą długość, a bok
AC ma długość
6 :
Wiedząc, że P_{\triangle ABC}=18\sqrt{3} , oblicz
P_{\triangle ABM} .
Odpowiedź:
Zadanie 7. 2 pkt ⋅ Numer: pp-20906 ⋅ Poprawnie: 31/71 [43%]
Rozwiąż
Podpunkt 7.1 (2 pkt)
« Pole powierzchni trójkąta jest równe
84 , a promień
okręgu wpisanego w ten trójkąt ma długość
4 .
Wiedząc, że długości boków tego trójkąta są kolejnymi liczbami naturalnymi, oblicz długość
najkrótszej wysokości tego trójkąta.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 8. 2 pkt ⋅ Numer: pp-20903 ⋅ Poprawnie: 19/36 [52%]
Rozwiąż
Podpunkt 8.1 (2 pkt)
W trapezie
ABCD ,
AB\parallel CD , poprowadzono przekątne,
które przecięły się w punkcie
E . Pola powierzchni trójkątów
ABE i
BCE są równe odpowiednio
48 i
30 .
Oblicz pole powierzchni trójkąta CDE .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 9. 2 pkt ⋅ Numer: pp-20765 ⋅ Poprawnie: 47/195 [24%]
Rozwiąż
Podpunkt 9.1 (2 pkt)
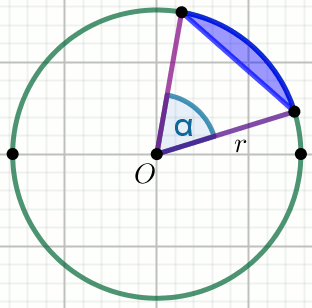
« Punkt
O jest środkiem okręgu. Oblicz pole
powierzchni niebieskiego obszaru:
Dane
r=2 \alpha=45^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 10. 2 pkt ⋅ Numer: pr-20770 ⋅ Poprawnie: 77/65 [118%]
Rozwiąż
Podpunkt 10.1 (2 pkt)
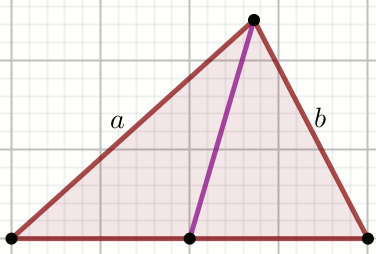
Dwa boki trójkąta mają długość
5 i
7 . Dowolny punkt boku trzeciego połączono
z wierzchołkiem kąta naprzeciwległego odcinkiem, który podzielił
ten trójkąta na dwa mniejsze trójkąty.
Oblicz stosunek długości promieni okręgów opisanych na otrzymanych
trójkątach. Podaj wartość tego stosunku należącą do przedziału
\langle 1,+\infty) .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 11. 4 pkt ⋅ Numer: pp-30398 ⋅ Poprawnie: 11/47 [23%]
Rozwiąż
Podpunkt 11.1 (1 pkt)
« Dwa boki trójkąta ostrokątnego mają długość
8 i
11 , a jego
pole powierzchni jest równe
22\sqrt{3} .
Oblicz miarę stopniową kąta zawartego między tymi bokami.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Oblicz długość trzeciego boku tego trójkąta.
Odpowiedź:
c=
\cdot √
(wpisz dwie liczby całkowite)
Podpunkt 11.3 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(liczba zapisana dziesiętnie)
Podpunkt 11.4 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(liczba zapisana dziesiętnie)
Zadanie 12. 4 pkt ⋅ Numer: pr-30348 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 12.1 (4 pkt)
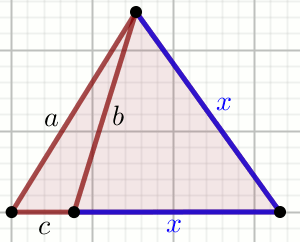
» Odcinki na rysunku maja długość:
a=32 ,
b=28 i
c=12 :
Oblicz obwód trójkąta na rysunku.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
Rozwiąż