Podgląd testu : lo2@sp-fun-wyk-log-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-11211 ⋅ Poprawnie: 162/263 [61%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wskaż argument, dla którego funkcja określona wzorem
f(x)=(\sqrt{3})^x
przyjmuje wartość 11:
Odpowiedzi:
| A. \log_{11}{11} | B. \frac{\log_{3}{11}}{2} |
| C. \log_{11}{9} | D. \log_{3}{11} |
| E. 11\cdot \log_{3}{121} | F. \log_{3}{121} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11201 ⋅ Poprawnie: 73/158 [46%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Funkcja g(x)=4^{5x+1} przyjmuje wartość:
Odpowiedzi:
| A. -\frac{\pi}{2} | B. -\sqrt{6} |
| C. \frac{\sqrt{5}}{5} | D. 0 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11193 ⋅ Poprawnie: 71/124 [57%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wykres funkcji g jest symetryczny do wykresu
funkcji f(x)=8^{-x} względem pewnej prostej.
Zatem g(x) jest równe:
Odpowiedzi:
| A. 8^{-x}-7 | B. \left(\frac{1}{7}\right)^{x} |
| C. -8^{-x} | D. -8^{x} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11219 ⋅ Poprawnie: 105/197 [53%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Dana jest funkcja f(x)=3^{x-7}-77.
Wyznacz miejsce zerowe funkcji określonej wzorem g(x)=f(x+1)-4.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pr-10160 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Oblicz sumę kwadratów miejsc zerowych funkcji określonej wzorem
g(x)=\log_{2\sqrt{2}}{(|x|-2)}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20580 ⋅ Poprawnie: 14/41 [34%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Funkcje f(x)=\left(\frac{1}{3}\right)^{x+a}-1
oraz g(x)=\log_{\frac{1}{2}}{(16+x+a)}+b\cdot p
mają to samo miejsce zerowe.
Oblicz to miejsce zerowe.
Dane
a=3
b=5
b=5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Podaj wartość parametru p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20559 ⋅ Poprawnie: 35/94 [37%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Rozwiąż nierówność:
\left(\frac{2}{3}\right)^{ax+2}\cdot \left(\frac{3}{2}\right)^{2ax+1} >
\left(\frac{27}{8}\right)^{ax-3}
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Dane
a=5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20309 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Rozwiąż równanie \log_{3}{x}=2-\log_{\frac{1}{3}}{2}.
Podaj największe rozwiązanie tego równania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 3 pkt ⋅ Numer: pr-30233 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Dana jest funkcja g(x)=|2^{x-1}-3| oraz
x_0=\log_{2}{a}+\log_{2}{a}\cdot \log_{a}{2}.
Oblicz g(x_0).
Dane
a=128
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Wyznacz te wartości x, dla których funkcja
g przyjmuje wartości większe od
g(x_0).
Podaj najmniejszą dodatnią liczbę całkowitą, która do tego zbioru nie należy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.3 (1 pkt)
Podaj największą dodatnią liczbę, która do tego zbioru nie należy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 4 pkt ⋅ Numer: pr-30231 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 10.1 (2 pkt)
Na rysunku pokazano wykres funkcji f(x)=-a^x+3.
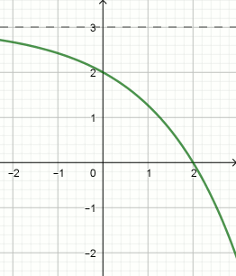

Wyznacz a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
Naszkicuj wykres funkcji
g(x)=a^{|x-3|}-1.
Podaj najmniejszą wartość funkcji g.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 4 pkt ⋅ Numer: pp-30176 ⋅ Poprawnie: 8/37 [21%] | Rozwiąż |
Podpunkt 11.1 (4 pkt)
« Rozwiąż nierówność
a^{1+6+11+...+(5x-4)} \leqslant b^c
.
Podaj największą liczbę całkowitą spełniającą tę nierówność.
Dane
a=8
b=512
c=9
b=512
c=9
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)