⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-fun-wyk-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-11211 ⋅ Poprawnie: 162/263 [61%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wskaż argument, dla którego funkcja określona wzorem
f(x)=(\sqrt{3})^x
przyjmuje wartość 5:
Odpowiedzi:
| A. \log_{5}{5} | B. \frac{\log_{3}{5}}{2} |
| C. \log_{3}{25} | D. \log_{3}{5} |
| E. \log_{5}{9} | F. 5\cdot \log_{3}{25} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11215 ⋅ Poprawnie: 205/370 [55%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dana jest funkcja f(x)=7^{x-5}.
Wskaż rozwiązanie nierówności f(x) > 0:
Odpowiedzi:
| A. (-5,+\infty) | B. \mathbb{R} |
| C. (-\infty,0\rangle | D. (0,+\infty) |
| E. (-\infty,0) | F. \langle 0,+\infty) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11217 ⋅ Poprawnie: 328/493 [66%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Funkcja wykładnicza g(x)=a^x jest malejąca oraz
g(-3)=64.
Wyznacz liczbę a.
Odpowiedź:
| a= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11190 ⋅ Poprawnie: 154/306 [50%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Wykres funkcji g(x)=-a^{x-b} zawiera punkt:
Dane
a=5
b=-5
b=-5
Odpowiedzi:
| A. A=(-5,25) | B. A=(-3,25) |
| C. A=(-5,-25) | D. A=(-3,-25) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11196 ⋅ Poprawnie: 360/519 [69%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
» Dana jest funkcja f(x)=a^x. Do jej wykresu
należy punkt o współrzędnych P=\left(-\frac{1}{5},2\right).
Wówczas liczba a jest równa \frac{1}{2^m}.
Podaj liczbę m.
Odpowiedź:
m=
(liczba zapisana dziesiętnie)
| Zadanie 6. 1 pkt ⋅ Numer: pp-11199 ⋅ Poprawnie: 97/210 [46%] | Rozwiąż |
Podpunkt 6.1 (0.2 pkt)
» Funkcja f(x)=(12\cdot m-7)^x jest rosnąca wtedy i tylko wtedy gdy
liczba m należy do pewnego przedziału.
Przedział ten ma postać:
Odpowiedzi:
| A. (-\infty,p\rangle | B. (-\infty,p) |
| C. (p, +\infty) | D. (p, q) |
| E. \langle p, q\rangle | F. \langle p, +\infty) |
Podpunkt 6.2 (0.8 pkt)
Podaj najmniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11208 ⋅ Poprawnie: 84/217 [38%] | Rozwiąż |
Podpunkt 7.1 (0.2 pkt)
Funkcja h(x)=(-7m-7)^x jest malejąca, wtedy i tylko wtedy, gdy
parametr m należy do pewnego zbioru.
Zbiór ten ma postać:
Odpowiedzi:
| A. \langle p, +\infty) | B. (-\infty, p) |
| C. (p, +\infty) | D. (-\infty, p\rangle |
| E. (-\infty, p)\cup(q, +\infty) | F. (p, q) |
Podpunkt 7.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów.
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
| min= | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11189 ⋅ Poprawnie: 97/141 [68%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Zbiór wartości funkcji f(x)=2^x+\sqrt{19}
zawiera liczbę:
Odpowiedzi:
| A. -20 | B. \sqrt{19}+2 |
| C. \sqrt{19}-2 | D. \frac{\sqrt{19}}{4} |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11192 ⋅ Poprawnie: 47/88 [53%] | Rozwiąż |
Podpunkt 9.1 (0.2 pkt)
» Dana jest funkcja g(x)=-3^{2-x}-8.
Zbiór ZW_g ma postać:
Odpowiedzi:
| A. \langle p, +\infty) | B. (-\infty,p) |
| C. \langle p, q\rangle | D. (p, q) |
| E. (-\infty, p)\cup(q, +\infty) | F. (-\infty, p\rangle |
Podpunkt 9.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów.
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
| min= | |
| Zadanie 10. 1 pkt ⋅ Numer: pp-11204 ⋅ Poprawnie: 208/479 [43%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Przesuwając wykres funkcji wykładniczej
f(x)=\left(\frac{1}{a}\right)^x o dwie jednostki
w prawo otrzymamy wykres funkcji g określonej wzorem:
Odpowiedzi:
| A. g(x)=\left(\frac{1}{10}\right)^{x}+2 | B. g(x)=100\cdot\left(\frac{1}{10}\right)^x |
| C. g(x)=10\cdot\left(\frac{1}{10}\right)^{x+1} | D. g(x)=\left(\frac{1}{10}\right)^{x}-2 |
| Zadanie 11. 1 pkt ⋅ Numer: pp-11206 ⋅ Poprawnie: 131/229 [57%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
» Wykres funkcji f(x)=\frac{1}{256}\cdot 4^x otrzymamy
przesuwając wykres funkcji g(x)=4^x o:
Odpowiedzi:
| A. cztery jednostki w lewo | B. cztery jednostki w prawo |
| C. dwie jednostki w górę | D. cztery jednostki w dół |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11212 ⋅ Poprawnie: 119/182 [65%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Dana jest funkcja f(x)=6^x+1.
Oblicz wartość funkcji określonej wzorem g(x)=f(x-2) dla argumentu x=7.
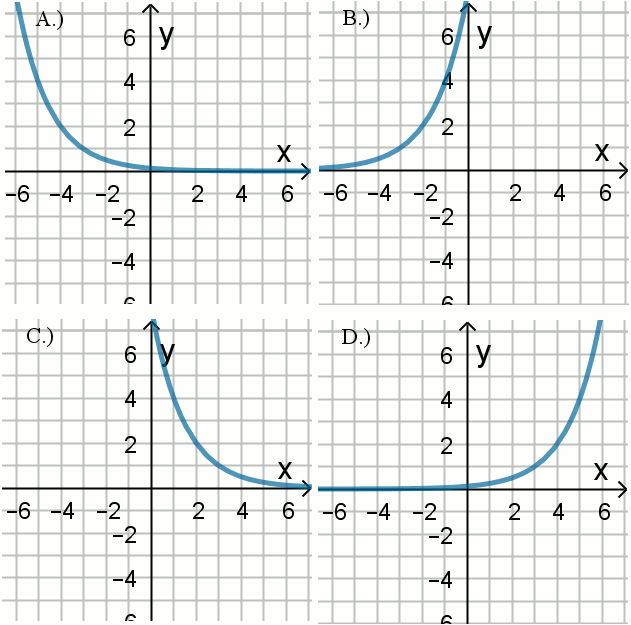
Odpowiedź:
g(7)=
(wpisz liczbę całkowitą)
| Zadanie 13. 1 pkt ⋅ Numer: pp-11202 ⋅ Poprawnie: 303/402 [75%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Do wykresu funkcji określonej wzorem f(x)=3^x+m należy punkt
o współrzędnych P=(5,-49).
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11205 ⋅ Poprawnie: 72/114 [63%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Do wykresu funkcji określonej wzorem f(x)=a^x należy punkt
o współrzędnych A=\left(\frac{3}{2},\frac{\sqrt{7}}{49}\right).
Wyznacz wartość parametru a.
Odpowiedź:
| a= | |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11210 ⋅ Poprawnie: 68/167 [40%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
« Równość f(x)=3, jeśli
f(x)=13^{2x}, zachodzi dla x=-\log_{13}{p}.
Podaj liczbę p.
Odpowiedź:
| p= | ||
| (wpisz trzy liczby całkowite) | ||