Podgląd testu : lo2@sp-geom-analit-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-11248 ⋅ Poprawnie: 222/346 [64%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Dany jest kwadrat ABCD. Punkty o współrzędnych
E=(4,-6) i F=(6,3) są
środkami dwóch jego boków odpowiednio AB i
BC. Zapisz długość przekątnej tego kwadratu w najprostszej postaci
a\sqrt{b}, gdzie a,b\in\mathbb{N}.
Podaj liczby a i b.
Odpowiedź:
d=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11228 ⋅ Poprawnie: 154/267 [57%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Obwód L rombu o sąsiednich wierzchołkach
A=(5,-8) i B=(8,4)
spełnia nierówność m\leqslant L\lessdot m+1, gdzie
m\in\mathbb{Z}.
Wyznacz liczbę m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11220 ⋅ Poprawnie: 183/331 [55%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Punkt M=\left(-\frac{3m}{2},7\right) jest środkiem odcinka o końcach
A=(6,5) i B=(-4,9).
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 4. 1 pkt ⋅ Numer: pr-10231 ⋅ Poprawnie: 1/1 [100%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Wierzchołkiem trójkąta równobocznego jest punkt o współrzędnych
A=(1,-3). Punkt P=(5,-3)
jest środkiem okręgu opisanego na tym trójkącie. W trójkąt ten wpisano okrąg o
równaniu (x-a)^2+(y-b)^2=r^2, gdzie.
r > 0.
Podaj liczby a, b i r.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| r | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. 1 pkt ⋅ Numer: pr-10201 ⋅ Poprawnie: 3/2 [150%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
» Do okręgu o równaniu (x-4)^2+(y+6)^2=\frac{m+1}{2}
należy punkt o współrzędnych (6,3).
Wyznacz wartość parametru m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20586 ⋅ Poprawnie: 24/88 [27%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Wyznacz rzedną punktu wspólnego osi Oy i symetralnej
odcinka o końcach A=(7,-5) i
B=(8,-7).
Podaj tę rzędną.
Odpowiedź:
| y= | |
| Zadanie 7. 2 pkt ⋅ Numer: pr-20385 ⋅ Poprawnie: 3/2 [150%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Punkty A=(4,9) i
B=(-8,-7) należą do okręgu, którego środek
należy do prostej y=x+3.
Podaj długość promienia tego okręgu.
Odpowiedź:
r=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Środkiem tego okręgu jest punkt S=(x_S,y_S).
Podaj x_S+y_S.
Odpowiedź:
x_S+y_S=
(wpisz liczbę całkowitą)
| Zadanie 8. 4 pkt ⋅ Numer: pr-30260 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
«« Punkt S=\left(\frac{25}{3},-\frac{13}{3}\right) jest środkiem ciężkości
trójkąta ABC, w którym
A=(2,-6) oraz
\overrightarrow{AB}=[7,0]. Wyznacz środek
D=(x_D,y_D) boku BC.
Podaj x_D.
Odpowiedź:
| x_D= | |
Podpunkt 8.2 (1 pkt)
Podaj y_D.
Odpowiedź:
| y_D= | |
Podpunkt 8.3 (1 pkt)
Wyznacz równanie boku BC: y=ax+b.
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
Podpunkt 8.4 (1 pkt)
Podaj miarę stopniową kąta rozwartego tego trójkąta.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 9. 4 pkt ⋅ Numer: pr-30278 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (2 pkt)
«« Czworokąt na rysunku jest rombem:
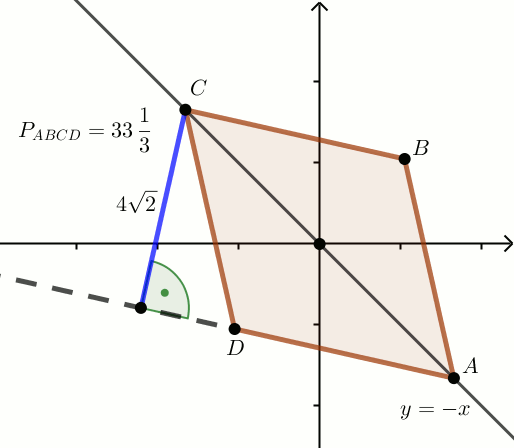

Wyznacz współrzędne wierzchołka A=(x_a,y_a).
Podaj x_a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (2 pkt)
Wyznacz współrzędne wierzchołka B=(x_b,y_b).
Podaj x_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)