⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-04-08-monotonicznosc-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10744 ⋅ Poprawnie: 182/387 [47%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Funkcja f opisana jest wzorem:
f(x)=x^2.
Wówczas:
Odpowiedzi:
| T/N : ZW_f=\left(0,+\infty\right) | T/N : f\left(-18\sqrt{2}\right)=-648 |
| T/N : wartości dodatnie funkcja ta przyjmuje tylko dla argumentów rożnych od zera | T/N : iloczyn x\cdot f(x) jest liczba dodatnią |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11533 ⋅ Poprawnie: 85/439 [19%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
(1 pkt)
Na rysunku pokazano wykres funkcji określonej wzorem y=f(x):
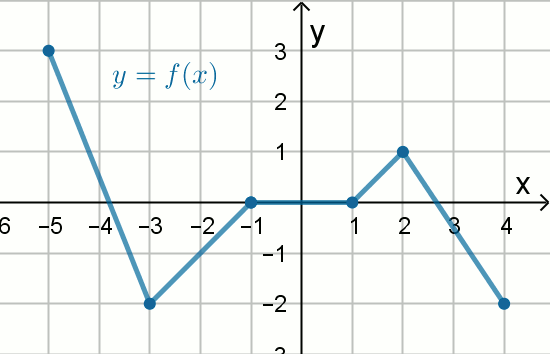
Wskaż zdanie fałszywe:
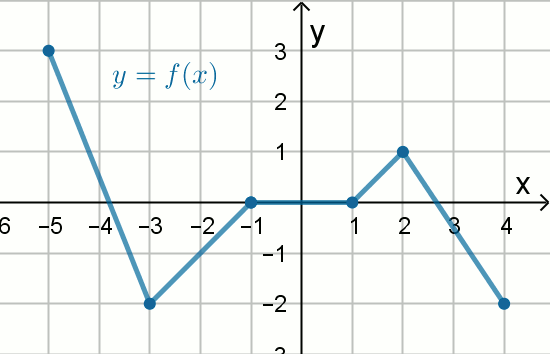
Odpowiedzi:
| A. funkcja jest rosnąca w co najmniej dwóch rozłącznych przedziałach | B. funkcja jest malejąca, gdy x\in\langle -5, -3\rangle\cup\langle 2, 4\rangle |
| C. ZW_{f}=\langle -2, 3\rangle | D. w przedziale \langle -3, 2\rangle funkcja jest monotoniczna |
| E. funkcja f nie jest różnowartościowa | F. funkcja f ma ujemne miejsce zerowe |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20292 ⋅ Poprawnie: 251/930 [26%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji f.
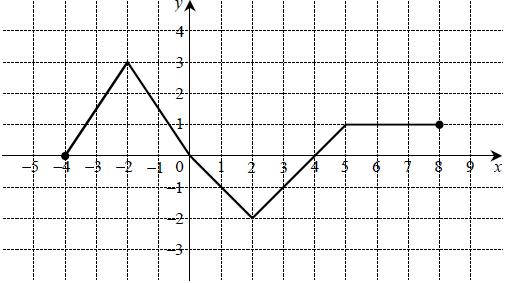
Ile liczb całkowitych należy do zbioru wartości tej funkcji?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Jaką długość ma przedział o maksymalnej długości, w którym funkcja ta jest monotoniczna?
Odpowiedź:
d=
(wpisz liczbę całkowitą)