Podgląd testu : lo2@zd-05-04-wlas-zadania-rozne-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10929 |
Podpunkt 1.1 (0.8 pkt)
Wykres funkcji liniowej określonej wzorem y=\frac{1}{10}(x+6)+4m-1
przecina dodatnią półoś Oy wtedy i tylko wtedy, gdy
parametr m należy do pewnego przedziału.
Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 1.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 5 | B. -6 |
| C. 8 | D. -7 |
| E. +\infty | F. -\infty |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10925 |
Podpunkt 2.1 (1 pkt)
Wykres funkcji liniowej
f(x)=\left(\frac{1}{2}m-6\right)x+\frac{1}{2}m+6
zawiera punkt M=(0,1).
Wyznacz m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10099 |
Podpunkt 3.1 (1 pkt)
» Na rysunku
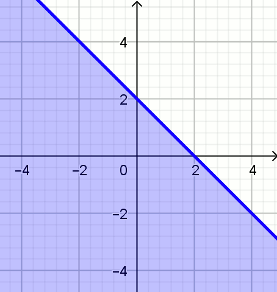
przedstawiony jest zbiór wszystkich punktów płaszczyzny, których współrzędne
spełniają nierówność:
Odpowiedzi:
| A. x-y-2\geqslant 0 | B. x-y+2\leqslant 0 |
| C. x+y+2\geqslant 0 | D. x+y-2\leqslant 0 |
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20311 |
Podpunkt 4.1 (2 pkt)
« Rozwiąż równanie 2x-2=\sqrt{2}x+8.
Podaj rozwiązanie.
Odpowiedź:
| x= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 5. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30049 |
Podpunkt 5.1 (2 pkt)
« Rozwiąż nierówność\frac{(x-1)^2}{3}-\frac{39}{2}<=\frac{16}{9}x-\frac{1-x}{2}\cdot \left(\frac{2}{3}x+3\right).
Podaj najmniejszą liczbe spęłniającą tę nierówność.
Odpowiedź:
| min= | |
Podpunkt 5.2 (2 pkt)
Najmniejszą liczbę spęłniającą tę nierówność zapisz w postaci ułamka
nieskracalnego o dodatnim mianowniku.
Podaj mianownik tego ułamka.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)