⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-08-05-tw-talesa-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10603 ⋅ Poprawnie: 229/386 [59%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{2},
|DC|=\frac{1}{4} i
|AB|=\frac{2}{3}:
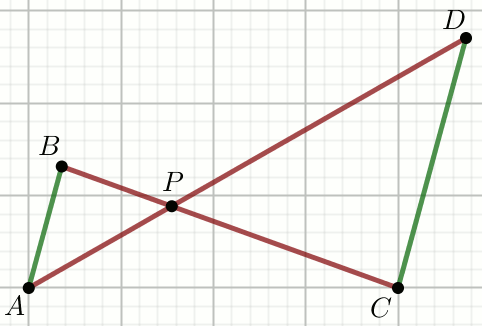
Oblicz długość odcinka DE.
Odpowiedź:
| |DE|= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10605 ⋅ Poprawnie: 170/279 [60%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{2},
|DE|=\frac{1}{4} i
|AB|=\frac{2}{3}:
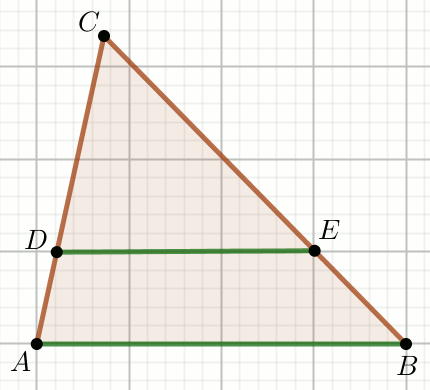
Oblicz długość odcinka DC.
Odpowiedź:
| |DC|= | |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20251 ⋅ Poprawnie: 94/262 [35%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{15}{4},
|AB|=6,
|AD|=3 i
|BC|=\frac{9}{4}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
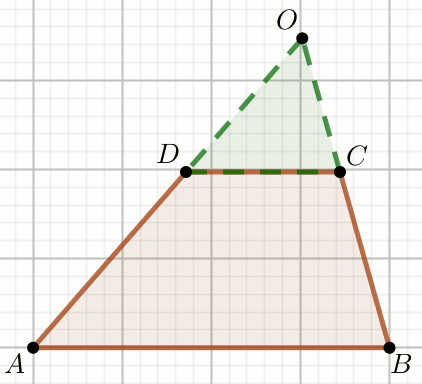
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 4. 2 pkt ⋅ Numer: pr-20026 ⋅ Poprawnie: 5/12 [41%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Zielony czworokąt na rysunku jest wpisany w trójkąt równoramienny
o podstawie długości 16 i ramieniu długości
17, jest prostokątem:
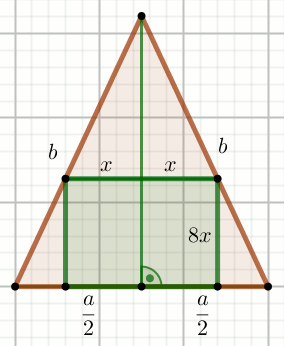
Oblicz jego obwód.
Odpowiedź:
| L= | |