⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-09-02-fun-kat-podst-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10674 ⋅ Poprawnie: 264/697 [37%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Przekątna równoległoboku o kącie ostrym \alpha o mierze
60^{\circ} i wysokości o długości
27\sqrt{3}, tworzy kąt prosty z jego bokiem.
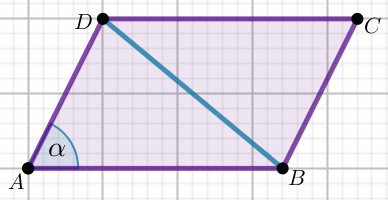
Oblicz obwód tego równoległoboku.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10657 ⋅ Poprawnie: 567/664 [85%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Przyprostokątne w trójkącie prostokątnym mają długości
1 oraz
\sqrt{3}.
Wyznacz miarę stopniową najmniejszego kąta w tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pp-20259 ⋅ Poprawnie: 165/275 [60%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Oblicz x-y, gdy
x=\sin^4{60^{\circ}}-\cos^4{60^{\circ}},
y=1-4\sin^2{60^{\circ}}\cdot \cos^2{60^{\circ}}.
Odpowiedź:
x-y=
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pp-20732 ⋅ Poprawnie: 176/451 [39%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
» Dany jest czworokąt, w którym \alpha=45^{\circ},
\beta=60^{\circ} i |DB|=7:
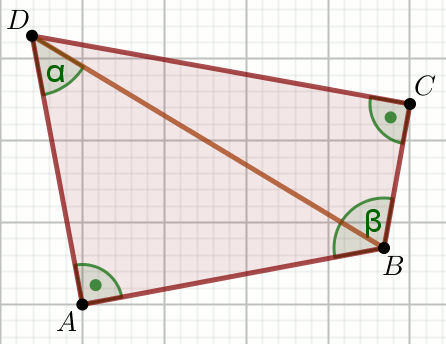
Oblicz długość obwodu czworokąta ABCD.
Odpowiedź:
L_{ABCD}=
(liczba zapisana dziesiętnie)