Podgląd testu : lo2@zd-13-03-okregi-i-kola-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10563 ⋅ Poprawnie: 96/155 [61%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Okręgi o takich samych promieniach mają środki w punktach
M=(-5, -10) i
N=(107, -25) i są wzajemnie styczne zewnętrznie.
Wyznacz długość promienia tych okręgów.
Odpowiedź:
| r= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11102 ⋅ Poprawnie: 26/118 [22%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W okrąg o promieniu długości 38 wpisano kąt środkowy
oparty na łuku długości równej 25% długości całego
okręgu. Następnie w ten kąt środkowy wpisano okrąg.
Oblicz długość promienia tego okręgu.
Odpowiedź:
r=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 3. 2 pkt ⋅ Numer: pp-20220 ⋅ Poprawnie: 68/111 [61%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Czworokąt na rysunku jest kwadratem:
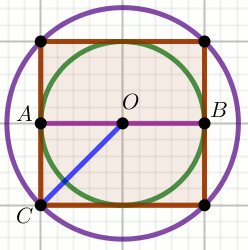

Oblicz |CO|:|AB|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 4 pkt ⋅ Numer: pp-30011 ⋅ Poprawnie: 10/34 [29%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
» Okręgi na rysunku są styczne do siebie i boków trójkąta równobocznego
o polu powierzchni P, a promień
r ma długość x\sqrt{y},
gdzie x,y\in\mathbb{N} i
y jest liczbą pierwszą:
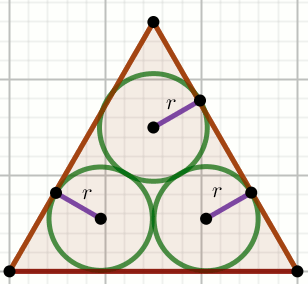

Wyznacz x.
Dane
P=648+432\sqrt{3}=1396.24594886975500
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.2 (2 pkt)
Wyznacz y.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)