⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-21-02-trapezy-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11086 ⋅ Poprawnie: 151/219 [68%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» W trapezie prostokątnym różnicą miar kątów wewnętrznych przy jednym z
ramion jest równa 30^{\circ}.
Największy kąt tego trapezu ma miarę \alpha.
Podaj \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 2. 2 pkt ⋅ Numer: pp-20435 ⋅ Poprawnie: 11/105 [10%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Czworokąt na rysunku jest trapezem równoramiennym, w którym suma
długości podstaw jest równa 626 oraz:
b=233:
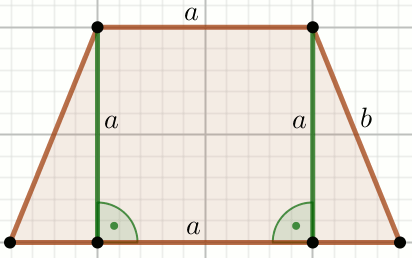
Podaj najmiejszą możliwą długość krótszej podstawy tego trapezu.
Odpowiedź:
a_{min}=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
Podaj największą możliwą długość dłuższej podstawy tego trapezu.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 3. 4 pkt ⋅ Numer: pp-30111 ⋅ Poprawnie: 7/87 [8%] | Rozwiąż |
Podpunkt 3.1 (4 pkt)
««« Dany jest trapez prostokątny ABCD, w którym
kąty przy wierzchołkach A i
D są proste oraz |AB|=9,
|DC|=7, a przekątna AC
jest dwa razy dłuższa od ramienia DA.
Na półprostej BA^{\rightarrow} obrano taki punkt
X, że
|CX|=|CB|.
Oblicz sinus kąta XCB.
Odpowiedź:
| \sin\sphericalangle XCB= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 4 pkt ⋅ Numer: pr-30094 ⋅ Poprawnie: 1/1 [100%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
Czworokąt na rysunku jest trapezem, w którym
|CD|=8,
|AD|=7 i
|AC|=13:
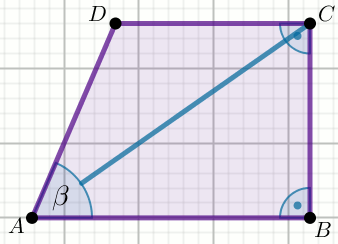
Oblicz \cos\beta.
Odpowiedź:
| \cos\beta= | |
Podpunkt 4.2 (2 pkt)
Jaką długość ma odcinek łączący środki jego ramion?
Odpowiedź:
| d= | |