⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-21-05-okrag-wpisany-pr
| Zadanie 1. 2 pkt ⋅ Numer: pr-20139 ⋅ Poprawnie: 79/73 [108%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
W trapez o obwodzie długości 54 i stosunku
ramion równym \frac{10}{17}, wpisano okrąg o promieniu długości
4.
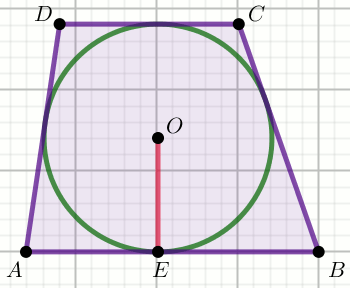
Podaj długość krótszej podstawy tego trapezu.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 1.2 (1 pkt)
Podaj długość dłuższej podstawy tego trapezu.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 2. 4 pkt ⋅ Numer: pr-30103 ⋅ Poprawnie: 120/114 [105%] | Rozwiąż |
Podpunkt 2.1 (4 pkt)
» Czworokąt na rysunku jest trapezem prostokątnym:
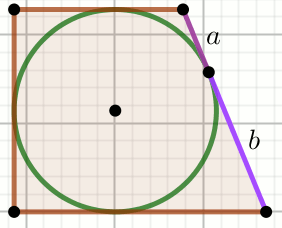
Oblicz obwód tego trapezu.
Dane
a=4
b=16
b=16
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 3. 4 pkt ⋅ Numer: pr-30109 ⋅ Poprawnie: 2/6 [33%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
» Czworokąt na rysunku jest trapezem równoramiennym, w którym
|OE|=18 oraz
|CE|=4x i |BE|=9x:
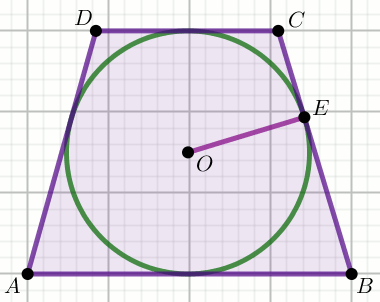
Oblicz x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (2 pkt)
Oblicz \cos \alpha, gdzie
\alpha jest kątem przy podstawie pomiędzy przekątną
trapezu a ramieniem tego trapezu.
Odpowiedź:
\cos\alpha=
(liczba zapisana dziesiętnie)