⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-22-04-czworokaty-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11088 ⋅ Poprawnie: 148/306 [48%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Pole powierzchni zacieniowanej części rysunku:
jest równe ......... cm2 .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pp-20851 ⋅ Poprawnie: 20/69 [28%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
W deltoid o obwodzie L=60 wpisano
okrąg o promieniu r=5:
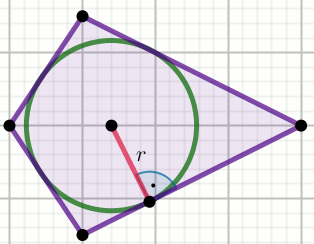
Oblicz pole powierzchni tego deltoidu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 4 pkt ⋅ Numer: pr-30136 ⋅ Poprawnie: 16/42 [38%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Dany jest czworokąt:
Oblicz \cos\beta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (2 pkt)
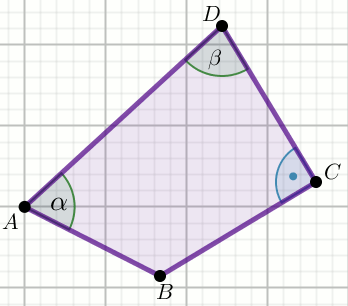
Oblicz pole powierzchni tego czworokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)