⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Rozwiązywanie nierówności metodą nierówności równoważnych
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- nierówności
- nierówności równoważne
- przekształcenia równoważne
- metoda nierówności równoważnych
- nierówności z jedną niewiadomą
| Zadanie 1. 1 pkt ⋅ Numer: pp-10001 ⋅ Poprawnie: 153/263 [58%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Które z podanych nierówności są sprzeczne:
Odpowiedzi:
| T/N : x^2+7 < -3 | T/N : -x^2-2 > 1 |
| T/N : x^4 > 81 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10081 ⋅ Poprawnie: 313/758 [41%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Wyznacz najmniejszą liczbę całkowitą spełniajacą nierówność
\frac{x-6}{8} \lessdot \frac{x-6}{6}+\frac{2}{3}.
Odpowiedź:
x_{min, \in\mathbb{Z}}=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10082 ⋅ Poprawnie: 297/506 [58%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Wyznacz najmniejszą liczbę całkowitą spełniajacą nierówność
\frac{3(x-6)-2}{7} \lessdot \frac{x-6}{2}
Odpowiedź:
x_{min, \in\mathbb{Z}}=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10083 ⋅ Poprawnie: 241/353 [68%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wyznacz najmniejszą liczbę spełniajacą nierówność
\frac{x-3}{2}\leqslant \frac{2x-6}{3}+\frac{1}{4}.
Odpowiedź:
| x_{min}= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10084 ⋅ Poprawnie: 163/311 [52%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Liczba k jest najmniejszą liczbą całkowitą, która
spełnia nierówność
\frac{x-6}{10}+\frac{\sqrt{7}}{2} >0 .
Podaj k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 6. 1 pkt ⋅ Numer: pp-10085 ⋅ Poprawnie: 359/512 [70%] | Rozwiąż |
Podpunkt 6.1 (0.8 pkt)
Rozwiąż nierówność
2(x-8)\leqslant 4(x-7)+1. Rozwiązanie zapisz w postaci przedziału.
Podaj ten koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| x_{\in\mathbb{Q},\notin\mathbb{Z}}= | |
Podpunkt 6.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -8 | B. +\infty |
| C. 6 | D. -\infty |
| E. 7 | F. -7 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10086 ⋅ Poprawnie: 205/319 [64%] | Rozwiąż |
Podpunkt 7.1 (0.8 pkt)
Rozwiąż nierówność
x-\sqrt{3}\lessdot 0. Rozwiązanie zapisz w postaci przedziału.
Podaj ten koniec przedziału, który jest liczbą niewymierną.
Odpowiedź:
| x_{\in\mathbb{NW}}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 7.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 7 | B. 6 |
| C. -7 | D. -8 |
| E. -\infty | F. +\infty |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10087 ⋅ Poprawnie: 118/266 [44%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Wyznacz ilość liczb całkowitych x, które spełniają nierówność
\frac{2}{9}\lessdot \frac{x}{18}\lessdot \frac{4}{3}.
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 9. 1 pkt ⋅ Numer: pp-10088 ⋅ Poprawnie: 634/871 [72%] | Rozwiąż |
Podpunkt 9.1 (0.8 pkt)
Zbiór wszystkich liczb rzeczywistych spełniających nierówność
\frac{3}{5}-\frac{2x-6}{3}\geqslant \frac{x-3}{6}
jest pewnym przedziałem.
Podaj ten koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 9.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. +\infty | B. 7 |
| C. 4 | D. -\infty |
| E. -6 | F. 5 |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10073 ⋅ Poprawnie: 191/322 [59%] | Rozwiąż |
Podpunkt 10.1 (0.2 pkt)
« Zbiorem rozwiązań nierówności
3+\frac{5-x}{3}-\frac{2x-7}{2} \lessdot x
jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. (-\infty, p\rangle | B. (p, q) |
| C. (p, +\infty) | D. (-\infty, p) |
| E. \langle p, q\rangle | F. \langle p, +\infty) |
Podpunkt 10.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 11. 1 pkt ⋅ Numer: pp-10074 ⋅ Poprawnie: 178/254 [70%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Wyznacz najmniejszą liczbę całkowitą spełniającą nierówność
\frac{x-3}{5}+\frac{5}{12} \lessdot \frac{7(x-3)}{15}.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
| Zadanie 12. 1 pkt ⋅ Numer: pp-10075 ⋅ Poprawnie: 329/426 [77%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Ile liczb całkowitych spełnia nierówność
\frac{x+3}{4}+\frac{1}{3} > \frac{x+3}{5}:
Odpowiedzi:
| A. nieskończenie wiele | B. 7 |
| C. 8 | D. 9 |
| E. 10 | F. 6 |
| Zadanie 13. 1 pkt ⋅ Numer: pp-10076 ⋅ Poprawnie: 237/339 [69%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Wyznacz największą liczbę całkowitą spełniającą nierówność
-3\leqslant 7-\frac{1}{3}x\leqslant 3.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 14. 1 pkt ⋅ Numer: pp-10077 ⋅ Poprawnie: 94/136 [69%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Liczba x spełnia nierówność
\frac{4}{x} > 4. Wynika z tego, że:
Odpowiedzi:
| A. x\in(0,1) | B. x\in(1,+\infty) |
| C. x\in(-\infty,0)\cup (0,1) | D. x\in(-\infty,0)\cup (1,+\infty) |
| Zadanie 15. 1 pkt ⋅ Numer: pp-10078 ⋅ Poprawnie: 141/216 [65%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
» Ile liczb naturalnych nie spełnia nierówności
\frac{1}{7}n\geqslant 2,5?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 16. 1 pkt ⋅ Numer: pp-10079 ⋅ Poprawnie: 184/337 [54%] | Rozwiąż |
Podpunkt 16.1 (0.2 pkt)
» Rozwiązaniem nierówności
\frac{x+4}{5}-\frac{x+3}{3}\geqslant 1
jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. \langle p, +\infty) | B. (-\infty, p\rangle |
| C. \langle p, q\rangle | D. (p, q) |
| E. (-\infty, p) | F. (p, +\infty) |
Podpunkt 16.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 17. 1 pkt ⋅ Numer: pp-11426 ⋅ Poprawnie: 268/387 [69%] | Rozwiąż |
Podpunkt 17.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{-3-2x}{2} > \frac{1}{3}
jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. \langle p, q\rangle | B. (-\infty, p) |
| C. \langle p, +\infty) | D. (p, q) |
| E. (-\infty, p\rangle | F. (p, +\infty) |
Podpunkt 17.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 18. 1 pkt ⋅ Numer: pp-10080 ⋅ Poprawnie: 120/156 [76%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
» Zbiorem rozwiązań nierówności
\sqrt{-x} \lessdot -3
jest:
Odpowiedzi:
| A. (-\infty,-3\rangle | B. (3,+\infty) |
| C. \emptyset | D. (-\infty,3\rangle |
| Zadanie 19. 1 pkt ⋅ Numer: pp-11530 ⋅ Poprawnie: 88/192 [45%] | Rozwiąż |
Podpunkt 19.1 (0.2 pkt)
Zbiorem rozwiązań nierówności
\frac{(3+\sqrt{11})(\sqrt{11}-3)\cdot x}{2}\leqslant 3x-\frac{4}{3}
jest pewien przedział liczbowy.
Przedział ten ma postać:
Odpowiedzi:
| A. (p, +\infty) | B. \langle p, q\rangle |
| C. \langle p, +\infty) | D. (p, q) |
| E. (-\infty, p\rangle | F. (-\infty, p) |
Podpunkt 19.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 20. 1 pkt ⋅ Numer: pp-10072 ⋅ Poprawnie: 383/584 [65%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
« Wyznacz największą liczbą całkowitą spełniającą nierówność
\frac{2(x-6)}{9}\geqslant \frac{x-6}{3}-\frac{1}{2}.
Odpowiedź:
x_{max,\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
| Zadanie 21. 1 pkt ⋅ Numer: pp-11761 ⋅ Poprawnie: 710/875 [81%] | Rozwiąż |
Podpunkt 21.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności
-2(x-2)\leqslant\frac{7-x}{3}
jest przedział:
Odpowiedzi:
| A. (-\infty,-1] | B. [-3,+\infty) |
| C. (-\infty,1] | D. [1,+\infty) |
| E. [-1,+\infty) | F. [3,+\infty) |
| Zadanie 22. 1 pkt ⋅ Numer: pp-11855 ⋅ Poprawnie: 249/337 [73%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności 1-\frac{x}{2}>\frac{x}{3},
jest przedział:
Odpowiedzi:
| A. \left(-\infty,\frac{6}{5}\right) | B. \left(-\frac{6}{5},+\infty\right) |
| C. \left(\frac{12}{5},+\infty\right) | D. \left(-\infty,-\frac{6}{5}\right) |
| E. \left(-\infty,\frac{3}{5}\right) | F. \left(-\infty,-\frac{12}{5}\right) |
| Zadanie 23. 1 pkt ⋅ Numer: pp-11883 ⋅ Poprawnie: 126/160 [78%] | Rozwiąż |
Podpunkt 23.1 (1 pkt)
Jedną z liczb spełniających nierówność x^4-3x^3-11\lessdot 0 jest:
Odpowiedzi:
| A. -3 | B. -6 |
| C. 4 | D. -4 |
| E. 2 | F. -2 |
| Zadanie 24. 1 pkt ⋅ Numer: pp-11912 ⋅ Poprawnie: 195/267 [73%] | Rozwiąż |
Podpunkt 24.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności \frac{3x-3}{4}>-6x
jest przedział:
Odpowiedzi:
| A. \left(\frac{1}{9},+\infty\right) | B. \left(-\infty,\frac{1}{27}\right) |
| C. \left(\frac{2}{27},+\infty\right) | D. \left(\frac{1}{6},+\infty\right) |
| E. \left(-\infty,\frac{1}{9}\right) | F. \left(-\infty,\frac{2}{9}\right) |
| Zadanie 25. 1 pkt ⋅ Numer: pp-11967 ⋅ Poprawnie: 42/60 [70%] | Rozwiąż |
Podpunkt 25.1 (1 pkt)
Dana jest nierówność
1-\frac{x}{2}\geqslant \frac{x}{3}+4.
Największą liczbą całkowitą, która spełnia tę nierówność jest:
Odpowiedzi:
| A. -8 | B. 2 |
| C. 0 | D. -3 |
| E. -9 | F. 1 |
| Zadanie 26. 1 pkt ⋅ Numer: pp-11984 ⋅ Poprawnie: 429/729 [58%] | Rozwiąż |
Podpunkt 26.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
-6-\frac{3}{2}x\lessdot \frac{2}{3}-x jest
przedział postaci:
Odpowiedzi:
| A. (a, +\infty) | B. (-\infty, a\rangle |
| C. \langle a, +\infty) | D. (-\infty, a) |
Podpunkt 26.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedzi:
| A. -\frac{160}{9} | B. -\frac{40}{3} |
| C. -10 | D. -\frac{80}{3} |
| E. -\frac{20}{3} | F. -8 |
| Zadanie 27. 1 pkt ⋅ Numer: pp-12007 ⋅ Poprawnie: 17/24 [70%] | Rozwiąż |
Podpunkt 27.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
-6-\frac{3}{2}x\lessdot \frac{2}{3}-x jest
przedział postaci:
Odpowiedzi:
| A. (a, +\infty) | B. \langle a, +\infty) |
| C. (-\infty, a\rangle | D. (-\infty, a) |
Podpunkt 27.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedzi:
| A. -\frac{160}{9} | B. -\frac{20}{3} |
| C. -\frac{80}{3} | D. -8 |
| E. -\frac{200}{9} | F. -\frac{40}{3} |
| Zadanie 28. 1 pkt ⋅ Numer: pp-12006 ⋅ Poprawnie: 381/447 [85%] | Rozwiąż |
Podpunkt 28.1 (1 pkt)
Liczba wszystkich całkowitych dodatnich rozwiązań nierówności
\frac{3x-26}{12}\lessdot \frac{1}{3} jest równa:
Odpowiedzi:
| A. 9 | B. 16 |
| C. 13 | D. 12 |
| E. 15 | F. 8 |
| Zadanie 29. 1 pkt ⋅ Numer: pp-12030 ⋅ Poprawnie: 43/57 [75%] | Rozwiąż |
Podpunkt 29.1 (1 pkt)
Zbiorem rozwiązań nierówności \frac{\frac{33}{4}-5x}{2}\lessdot 3\left(\frac{5}{8}-\frac{1}{2}x\right)+7x+\frac{21}{4} jest:
Odpowiedzi:
| A. \left(-\infty,\frac{11}{8}\right) | B. \left(-\infty,\frac{9}{8}\right) |
| C. \left(-\frac{3}{8},+\infty\right) | D. \left(-\frac{1}{4},+\infty\right) |
| E. \left(-\frac{1}{8},+\infty\right) | F. \left(-\frac{1}{2},+\infty\right) |
| Zadanie 30. 1 pkt ⋅ Numer: pp-12057 ⋅ Poprawnie: 37/48 [77%] | Rozwiąż |
Podpunkt 30.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{6-x}{2}-6x\geqslant 1 jest:
Odpowiedzi:
| A. \left(-\infty,\frac{6}{13}\right] | B. \left[\frac{4}{13},+\infty\right) |
| C. \left(-\infty,\frac{8}{13}\right] | D. \left(-\infty,\frac{8}{39}\right] |
| E. \left[\frac{4}{13},+\infty\right) | F. \left(-\infty,\frac{4}{13}\right) |
| Zadanie 31. 1 pkt ⋅ Numer: pp-12085 ⋅ Poprawnie: 25/44 [56%] | Rozwiąż |
Podpunkt 31.1 (1 pkt)
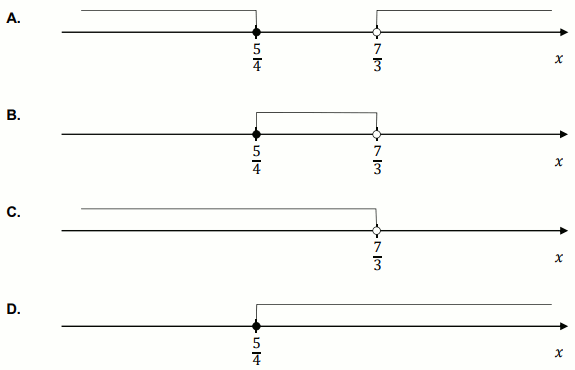
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych
x, spełniających alternatywę nierówności
0 > 7-3x lub
7-3x\geqslant 5x-3:
Odpowiedzi:
| A. C | B. B |
| C. A | D. D |
| Zadanie 32. 0.2 pkt ⋅ Numer: pp-12112 ⋅ Poprawnie: 41/48 [85%] | Rozwiąż |
Podpunkt 32.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności 5-\frac{2-3x}{4}\geqslant -6x+1
jest zbiór:
Odpowiedzi:
| A. \left[-\frac{28}{27}, +\infty\right) | B. \left[-\frac{14}{27}, +\infty\right) |
| C. \left[-\frac{7}{27}, +\infty\right) | D. \left(-\infty, \frac{14}{27}\right] |
| E. \left(-\infty, -\frac{14}{27}\right] | F. \left[\frac{7}{27}, +\infty\right) |
| Zadanie 33. 1 pkt ⋅ Numer: pp-12138 ⋅ Poprawnie: 173/194 [89%] | Rozwiąż |
Podpunkt 33.1 (0.2 pkt)
Zbiorem wszystkich rozwiązań nierówności
\frac{-8(-4-x)}{5}\leqslant 8 jest
przedział postaci:
Odpowiedzi:
| A. (-\infty, a) | B. (a, +\infty) |
| C. (-\infty, a] | D. [a, +\infty) |
Podpunkt 33.2 (0.8 pkt)
Liczba a jest równa:
Odpowiedzi:
| A. 1 | B. 2 |
| C. \frac{4}{3} | D. \frac{1}{2} |
| E. \frac{3}{2} | F. \frac{3}{4} |
| Zadanie 34. 1 pkt ⋅ Numer: pp-12386 ⋅ Poprawnie: 560/475 [117%] | Rozwiąż |
Podpunkt 34.1 (1 pkt)
Zbiorem wszystkich rozwiązań nierówności 9-2(1-13x\geqslant 2x-17
jest przedział:
Odpowiedzi:
| A. [-1, +\infty) | B. (-\infty, -4] |
| C. (-\infty, 3] | D. [-3, +\infty) |
| E. [0, +\infty) | F. (-\infty, -3] |
| Zadanie 35. 1 pkt ⋅ Numer: pp-12406 ⋅ Poprawnie: 341/359 [94%] | Rozwiąż |
Podpunkt 35.1 (1 pkt)
Dana jest nierówność -3-\frac{-5-2x}{2}\geqslant 3x.
Największą liczbą całkowitą, która spełnia tę nierówność, jest:
Odpowiedzi:
| A. 2 | B. -4 |
| C. 3 | D. -3 |
| E. -2 | F. -1 |
| G. -6 | H. 5 |
| Zadanie 36. 2 pkt ⋅ Numer: pp-20018 ⋅ Poprawnie: 90/156 [57%] | Rozwiąż |
Podpunkt 36.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
x(6-x)\lessdot (4-x)(x+4)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 37. 2 pkt ⋅ Numer: pp-20023 ⋅ Poprawnie: 85/143 [59%] | Rozwiąż |
Podpunkt 37.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
(3-x)(3-x)\geqslant (x+1)(x-4)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 38. 2 pkt ⋅ Numer: pp-20024 ⋅ Poprawnie: 70/145 [48%] | Rozwiąż |
Podpunkt 38.1 (2 pkt)
« Rozwiąż nierówność z niewiadomą x:
(x+2)(x-3)\lessdot(2-x)(3-x)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 39. 2 pkt ⋅ Numer: pp-20025 ⋅ Poprawnie: 110/175 [62%] | Rozwiąż |
Podpunkt 39.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
(x+4)^2 >(x+2)^2
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 40. 2 pkt ⋅ Numer: pp-20026 ⋅ Poprawnie: 126/253 [49%] | Rozwiąż |
Podpunkt 40.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
(4-x)(x+4)\leqslant 1-(x+3)^2
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 41. 2 pkt ⋅ Numer: pp-20027 ⋅ Poprawnie: 88/137 [64%] | Rozwiąż |
Podpunkt 41.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
(4+x)^2 \lessdot (x-3)(x+3)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 42. 2 pkt ⋅ Numer: pp-20028 ⋅ Poprawnie: 212/300 [70%] | Rozwiąż |
Podpunkt 42.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
2(x-3)-(4-3x) > 3x+6
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 43. 2 pkt ⋅ Numer: pp-20029 ⋅ Poprawnie: 81/115 [70%] | Rozwiąż |
Podpunkt 43.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
(x-1)^2-2x \geqslant -6-(2+x)(2-x)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 44. 2 pkt ⋅ Numer: pp-20030 ⋅ Poprawnie: 48/84 [57%] | Rozwiąż |
Podpunkt 44.1 (2 pkt)
« Rozwiąż nierówność z niewiadomą x:
3(x+2)-(2-5x) > 2x+6
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 45. 2 pkt ⋅ Numer: pp-20019 ⋅ Poprawnie: 91/152 [59%] | Rozwiąż |
Podpunkt 45.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
(x-2)^2\leqslant (x+3)(x-3)-6
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 46. 2 pkt ⋅ Numer: pp-20020 ⋅ Poprawnie: 72/93 [77%] | Rozwiąż |
Podpunkt 46.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
2x^2+2x+6 > 2(x-3)(x-1)
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 47. 2 pkt ⋅ Numer: pp-20021 ⋅ Poprawnie: 113/209 [54%] | Rozwiąż |
Podpunkt 47.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
5(2-x)-2(x-6)\geqslant -(x-5)
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 48. 2 pkt ⋅ Numer: pp-20022 ⋅ Poprawnie: 140/255 [54%] | Rozwiąż |
Podpunkt 48.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
12(3-x)-(8x-6)\leqslant 5(6-2x)
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 49. 2 pkt ⋅ Numer: pp-20031 ⋅ Poprawnie: 116/180 [64%] | Rozwiąż |
Podpunkt 49.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{x+4}{2}\leqslant \frac{2x+8}{3}+\frac{1}{4}
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| lewy= | |
| Zadanie 50. 2 pkt ⋅ Numer: pp-20042 ⋅ Poprawnie: 75/99 [75%] | Rozwiąż |
Podpunkt 50.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
\frac{x+4}{4}+\frac{1}{6}\lessdot\frac{x+4}{3}
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| lewy= | |
| Zadanie 51. 2 pkt ⋅ Numer: pp-20046 ⋅ Poprawnie: 76/170 [44%] | Rozwiąż |
Podpunkt 51.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
\frac{2}{3}-\frac{3(x-4)}{5}\lessdot 7
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
lewy=
(liczba zapisana dziesiętnie)
| Zadanie 52. 2 pkt ⋅ Numer: pp-20047 ⋅ Poprawnie: 97/135 [71%] | Rozwiąż |
Podpunkt 52.1 (2 pkt)
« Rozwiąż nierówność z niewiadomą x:
x-\frac{7}{8}(x-4) \lessdot \frac{-4+x}{4}+4
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| lewy= | |
| Zadanie 53. 2 pkt ⋅ Numer: pp-20048 ⋅ Poprawnie: 82/93 [88%] | Rozwiąż |
Podpunkt 53.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{3}{8}+\frac{x}{18}\lessdot \frac{5x}{36}
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| lewy= | |
| Zadanie 54. 2 pkt ⋅ Numer: pp-20049 ⋅ Poprawnie: 46/91 [50%] | Rozwiąż |
Podpunkt 54.1 (2 pkt)
« Rozwiąż nierówność z niewiadomą x:
\frac{x}{6}+1 \leqslant \frac{x}{3\sqrt{2}}+\frac{1}{2}
.
Rozwiązanie zapisz w postaci przedziału. Lewy koniec tego przedziału jest liczbą postaci \frac{m}{\sqrt{2}-1}. Podaj liczbę m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 55. 2 pkt ⋅ Numer: pp-20050 ⋅ Poprawnie: 53/88 [60%] | Rozwiąż |
Podpunkt 55.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
2(-1-x)-\frac{x+2}{4} > \frac{-3-x}{2}
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| prawy= | |
| Zadanie 56. 2 pkt ⋅ Numer: pp-20051 ⋅ Poprawnie: 161/221 [72%] | Rozwiąż |
Podpunkt 56.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{2x+3}{6}- \frac{x+6}{3} \lessdot 1
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego prawy koniec.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 57. 2 pkt ⋅ Numer: pp-20052 ⋅ Poprawnie: 60/75 [80%] | Rozwiąż |
Podpunkt 57.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{3x}{2}-\frac{2x}{3}-\frac{x}{6} \lessdot -6
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| prawy= | |
| Zadanie 58. 2 pkt ⋅ Numer: pp-20032 ⋅ Poprawnie: 74/97 [76%] | Rozwiąż |
Podpunkt 58.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{x-1}{2}-\frac{x}{4}\geqslant \frac{x}{6}+\frac{-6-x}{3}
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| lewy= | |
| Zadanie 59. 2 pkt ⋅ Numer: pp-20033 ⋅ Poprawnie: 74/87 [85%] | Rozwiąż |
Podpunkt 59.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
2(-6+2x)+3(1-3x)>\frac{7-10x}{2}
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego koniec liczbowy.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 60. 2 pkt ⋅ Numer: pp-20034 ⋅ Poprawnie: 55/76 [72%] | Rozwiąż |
Podpunkt 60.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{5}{2}x+6 \leqslant \frac{3+5x}{3}+\frac{5x}{6}
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego koniec liczbowy.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 61. 2 pkt ⋅ Numer: pp-20035 ⋅ Poprawnie: 66/77 [85%] | Rozwiąż |
Podpunkt 61.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{3}{8}x+\frac{5x-3}{12} \lessdot \frac{x}{6}-\frac{-6-5x}{8}
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego koniec liczbowy.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 62. 2 pkt ⋅ Numer: pp-20036 ⋅ Poprawnie: 122/174 [70%] | Rozwiąż |
Podpunkt 62.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
3(2-\frac{1}{6}x)\geqslant -0,5x-6
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego prawy koniec.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 63. 2 pkt ⋅ Numer: pp-20037 ⋅ Poprawnie: 67/90 [74%] | Rozwiąż |
Podpunkt 63.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
-\frac{2}{3}(3x-2) > \frac{1}{2}(-6-4x)
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego prawy koniec.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 64. 2 pkt ⋅ Numer: pp-20038 ⋅ Poprawnie: 40/52 [76%] | Rozwiąż |
Podpunkt 64.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{x-2}{2} \lessdot \frac{3x-4}{6}+6
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego lewy koniec.
Odpowiedź:
x_L=
(wpisz liczbę całkowitą)
| Zadanie 65. 2 pkt ⋅ Numer: pp-20039 ⋅ Poprawnie: 49/63 [77%] | Rozwiąż |
Podpunkt 65.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{4-5x}{3}\geqslant \frac{2-5x}{5}-6
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego prawy koniec.
Odpowiedź:
| x_P= | |
| Zadanie 66. 2 pkt ⋅ Numer: pp-20040 ⋅ Poprawnie: 60/79 [75%] | Rozwiąż |
Podpunkt 66.1 (2 pkt)
« Rozwiąż nierówność z niewiadomą x:
\frac{x-3}{2} \lessdot \frac{2x-6}{3}-\frac{2x-2}{6}
.
Jeżeli nierówność jest sprzeczna wpisz -1. Jeżeli nierówność jest tożsamościowa wpisz -2. Jeżeli rozwiązaniem jest przedział wpisz jego prawy koniec.
Odpowiedź:
x_P=
(wpisz liczbę całkowitą)
| Zadanie 67. 2 pkt ⋅ Numer: pp-20041 ⋅ Poprawnie: 53/104 [50%] | Rozwiąż |
Podpunkt 67.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{2x-6}{2}-\frac{13-6x}{6}\leqslant \frac{2x+1}{3}
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 68. 2 pkt ⋅ Numer: pp-20043 ⋅ Poprawnie: 77/104 [74%] | Rozwiąż |
Podpunkt 68.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{x-0,5}{3}\geqslant \frac{6x+6}{2}-\frac{2x-1}{3}
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 69. 2 pkt ⋅ Numer: pp-20044 ⋅ Poprawnie: 55/85 [64%] | Rozwiąż |
Podpunkt 69.1 (2 pkt)
Rozwiąż nierówność z niewiadomą x:
\frac{-6-4x}{6}\geqslant 3-\frac{5x-6}{2}
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
| Zadanie 70. 2 pkt ⋅ Numer: pp-20045 ⋅ Poprawnie: 46/59 [77%] | Rozwiąż |
Podpunkt 70.1 (2 pkt)
» Rozwiąż nierówność z niewiadomą x:
\frac{2x-6}{2}-1 \lessdot \frac{2x+6}{3}-4
.
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 71. 2 pkt ⋅ Numer: pp-20053 ⋅ Poprawnie: 49/93 [52%] | Rozwiąż |
Podpunkt 71.1 (1 pkt)
Wyznacz zbiór tych wartości x, dla których
prawdziwy jest warunek:
3x-2\in (-5,4)
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
Podpunkt 71.2 (1 pkt)
Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 72. 2 pkt ⋅ Numer: pp-20054 ⋅ Poprawnie: 43/69 [62%] | Rozwiąż |
Podpunkt 72.1 (1 pkt)
Wyznacz zbiór tych wartości x, dla których
prawdziwy jest warunek:
1-2x\in \langle -5,2\rangle
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
| x_L= | |
Podpunkt 72.2 (1 pkt)
Podaj prawy koniec tego przedziału.
Odpowiedź:
| x_P= | |
| Zadanie 73. 2 pkt ⋅ Numer: pp-20055 ⋅ Poprawnie: 76/159 [47%] | Rozwiąż |
Podpunkt 73.1 (2 pkt)
» Wyznacz zbiór tych wartości x, które spełniają
obie nierówności:
9x+80 > 7x+66 \quad\wedge\quad -13-4x \lessdot 3x+22
.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
x_L=
(wpisz liczbę całkowitą)
| Zadanie 74. 2 pkt ⋅ Numer: pp-20056 ⋅ Poprawnie: 47/83 [56%] | Rozwiąż |
Podpunkt 74.1 (2 pkt)
» Wyznacz zbiór tych wartości x, które spełniają
nierówność podwójną:
\frac{x+7}{3} \leqslant \frac{2x+17}{2} \lessdot \frac{3x+26}{4}
.
Podaj najmniejszą liczbę spełniającą tę nierówność. Jeśli nierówność jest sprzeczna, wpisz liczbę zero.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 75. 2 pkt ⋅ Numer: pp-20057 ⋅ Poprawnie: 50/78 [64%] | Rozwiąż |
Podpunkt 75.1 (2 pkt)
» Wyznacz zbiór tych wartości x, które spełniają
obie nierówności:
\frac{x}{10}-\frac{x}{8}+0,1\leqslant 0 \quad\wedge\quad
\frac{x-6}{8}\leqslant \frac{x-4}{6}
.
Podaj najmniejszą liczbę spełniającą obie nierówności.
Odpowiedź:
| x_{min}= | |
| Zadanie 76. 2 pkt ⋅ Numer: pp-20014 ⋅ Poprawnie: 30/41 [73%] | Rozwiąż |
Podpunkt 76.1 (2 pkt)
Przedział (-\infty,4\rangle jest rozwiązaniem
nierówności mx+7\geqslant 0.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 77. 2 pkt ⋅ Numer: pp-20015 ⋅ Poprawnie: 63/131 [48%] | Rozwiąż |
Podpunkt 77.1 (2 pkt)
Rozwiąż nierówność
\frac{x-\frac{3}{4}}{2}-\frac{x-\frac{5}{4}}{6}\geqslant \frac{\frac{7}{4}-x}{3}
.
Podaj najmniejszą liczbę spełniającą tę nierówność. Jeśli taka liczba nie istnieje wpisz 0.
Odpowiedź:
| x_{min}= | |
| Zadanie 78. 2 pkt ⋅ Numer: pp-20017 ⋅ Poprawnie: 15/42 [35%] | Rozwiąż |
Podpunkt 78.1 (2 pkt)
Dane są zbiory: A- zbiór liczb spełniających
nierówność -\frac{5}{2} \lessdot 1-\frac{1}{6}x \lessdot 3,
B - zbiór liczb spełniających nierówność
8\leqslant 3x-2\leqslant 11.
Wyznacz zbiór A-B.
Ile liczb całkowitych parzystych należy do tego zbioru?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 79. 2 pkt ⋅ Numer: pp-20001 ⋅ Poprawnie: 47/123 [38%] | Rozwiąż |
Podpunkt 79.1 (2 pkt)
« Rozwiąż nierówność
\frac{5}{x} > \frac{1}{2}.
Podaj najmniejszą liczbę dodatnią, która nie spełnia tej nierówności.
Odpowiedź:
min_{> 0}=
(wpisz liczbę całkowitą)
| Zadanie 80. 2 pkt ⋅ Numer: pp-20002 ⋅ Poprawnie: 57/120 [47%] | Rozwiąż |
Podpunkt 80.1 (2 pkt)
» Rozwiąż nierówność -\frac{42}{2x}\geqslant 3.
Ile liczb całkowitych spełnia tę nierówność?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 81. 2 pkt ⋅ Numer: pp-20003 ⋅ Poprawnie: 62/110 [56%] | Rozwiąż |
Podpunkt 81.1 (2 pkt)
Rozwiąż nierówność \frac{22}{x+4}\geqslant 2.
Podaj największą liczbę całkowitą, która spełnią tę nierówność.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 82. 4 pkt ⋅ Numer: pp-30003 ⋅ Poprawnie: 35/63 [55%] | Rozwiąż |
Podpunkt 82.1 (2 pkt)
» Dane są nierówności:
\left(\frac{1}{2}x-2\right)^2\geqslant 7-\left(2+0,5x\right)\left(-0,5x+2\right)
i x^2-7 \lessdot 0.
Ile liczb całkowitych spełnia jednocześnie obie nierówności?
Odpowiedź:
ile_{\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
Podpunkt 82.2 (2 pkt)
Ile wynosi suma tych liczb?
Odpowiedź:
suma_{\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
| Zadanie 83. 4 pkt ⋅ Numer: pp-30310 ⋅ Poprawnie: 35/59 [59%] | Rozwiąż |
Podpunkt 83.1 (1 pkt)
« Dane są zbiory: A- zbiór rozwiązań nierówności
\frac{3}{2}-\frac{3}{4}x > 0, B -
zbiór rozwiązań nierówności -3x\leqslant 15,
D=\langle -8,9\rangle. Wyznacz zbiór
A\cap B.
Podaj lewy koniec wyznaczonego przedziału.
Odpowiedź:
| x_L= | |
Podpunkt 83.2 (1 pkt)
Podaj prawy koniec wyznaczonego przedziału.
Odpowiedź:
| x_P= | |
Podpunkt 83.3 (2 pkt)
Ile liczb naturalnych należy do zbioru D-A?
Odpowiedź:
ile_{\in D-A}=
(wpisz liczbę całkowitą)