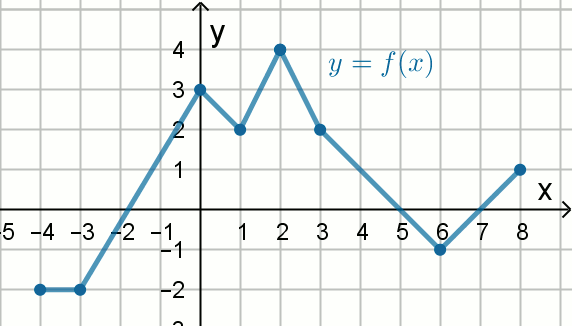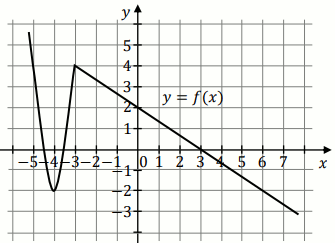Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Zbiór wartości funkcji

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10721 ⋅ Poprawnie: 219/402 [54%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
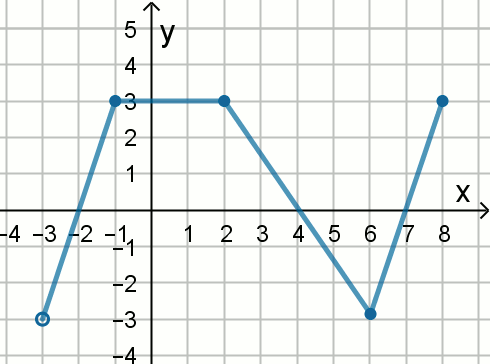
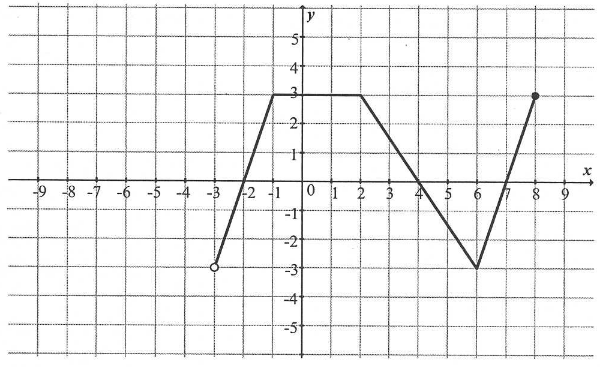
 « Wykres funkcji f pokazano na rysunku:

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : \frac{1}{f(1)} > f(4) T/N : f(3) > \left[f(3)\right]^2
Zadanie 2.  1 pkt ⋅ Numer: pp-10722 ⋅ Poprawnie: 435/771 [56%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
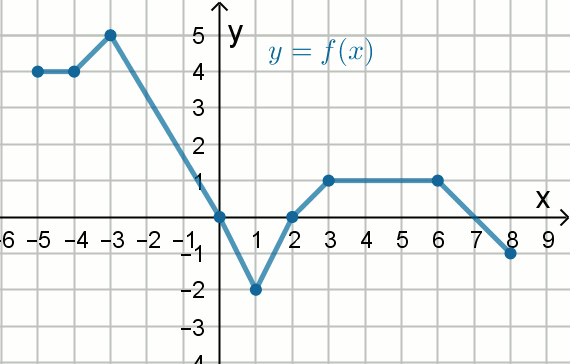
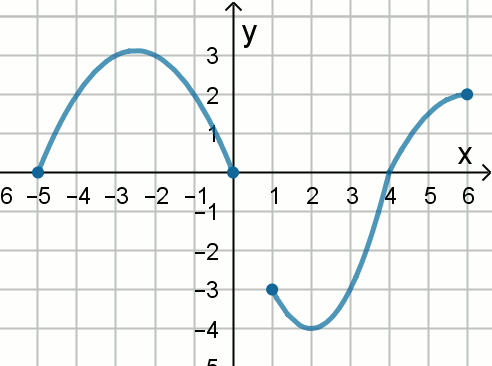
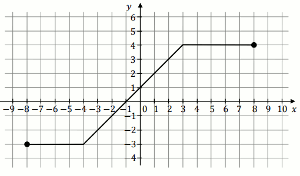
 « Wykres funkcji f pokazano na rysunku:

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : f(2)\lessdot f(8) T/N : f(5) > f(-5)
T/N : f(0) > f(7)  
Zadanie 3.  1 pkt ⋅ Numer: pp-10720 ⋅ Poprawnie: 216/296 [72%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=\frac{-4x+15}{x} dla każdej liczby rzeczywistej x\neq 0. Oblicz wartość funkcji f\left(\sqrt{5}\right). Wynik zapisz w najprostszej postaci a+b\sqrt{c}, gdzie a,b\in\mathbb{Z}, c\in\mathbb{N} i jest najmniejsze możliwe.
Odpowiedź:
Wpisz odpowiedź:  + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 4.  1 pkt ⋅ Numer: pp-10758 ⋅ Poprawnie: 180/291 [61%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 « Dla argumentu x=\frac{1}{\sqrt{8}-1} oblicz wartość funkcji określonej wzorem f(x)=-2x+4 i zapisz wynik w najprostszej postaci \frac{m+n\sqrt{k}}{p}, gdzie m,n,k,p\in\mathbb{Z}.

Podaj liczby m, n, k i p.

Odpowiedź:
\frac{m+n\sqrt{k}}{p}= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-10704 ⋅ Poprawnie: 280/415 [67%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=\frac{5x}{x+1} dla x\neq -1.

Oblicz wartość funkcji f dla argumentu x=\sqrt{6}. Wynik zapisz w najprostszej nieskracalnej postaci \frac{a+b\sqrt{c}}{d}, gdzie a,b\in\mathbb{Z}, c,d\in\mathbb{N}.

Odpowiedź:
Wpisz odpowiedź:  + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 6.  1 pkt ⋅ Numer: pp-10707 ⋅ Poprawnie: 599/798 [75%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
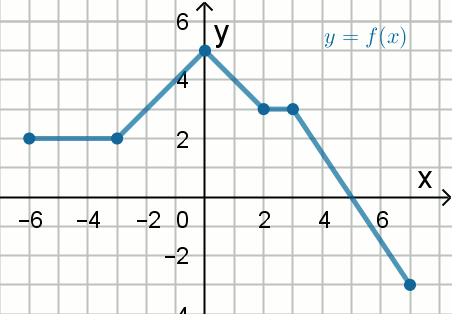
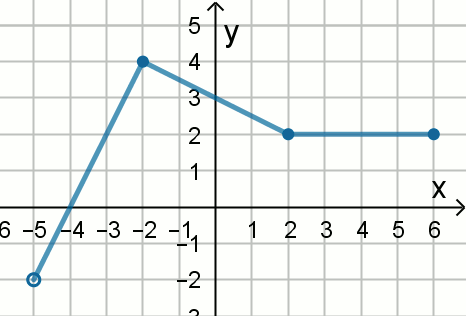
Liczby f_{min} i f_{max} sa odpowiednio najmniejszą i największą wartością funkcji, której wykres pokazano na rysunku:

Podaj liczby f_{min} i f_{max}.

Odpowiedzi:
f_{min}= (wpisz liczbę całkowitą)
f_{max}= (wpisz liczbę całkowitą)
Zadanie 7.  1 pkt ⋅ Numer: pp-10718 ⋅ Poprawnie: 35/90 [38%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 Zbiorem wartości funkcji określonej wzorem y=f(x) jest przedział \langle -3,8). Natomiast zbiorem wartości funkcji y=-4\cdot f(x) jest pewien inny przedział, w którym min jest najmniejszą liczbą całkowitą, a max największą liczbą całkowitą.

Podaj liczby min i max.

Odpowiedzi:
min= (wpisz liczbę całkowitą)
max= (wpisz liczbę całkowitą)
Zadanie 8.  1 pkt ⋅ Numer: pp-10761 ⋅ Poprawnie: 128/238 [53%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 « Dana jest funkcja określona wzorem g(x)=-\frac{14-2x}{x}. Połowę liczby g\left(\sqrt{2}\right) zapisz w postaci \frac{m+n\sqrt{k}}{p}, gdzie m,n,k,p\in\mathbb{Z}.
Odpowiedź:
\frac{m+n\sqrt{k}}{p}= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 9.  1 pkt ⋅ Numer: pp-10702 ⋅ Poprawnie: 159/224 [70%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Funkcja f określona jest wzorem f(x)=\frac{2x^3}{x^4+3} dla każdej liczby rzeczywistej x. Zapisz liczbę f\left(-\sqrt{6}\right) w najprostszej nieskracalnej postaci \frac{a\sqrt{b}}{c}, gdzie a\in\mathbb{Z} i b,c\in\mathbb{N}.
Odpowiedź:
Wpisz odpowiedź:  \cdot√
(wpisz trzy liczby całkowite)
Zadanie 10.  1 pkt ⋅ Numer: pp-10712 ⋅ Poprawnie: 117/160 [73%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 « Funkcja f określona jest wzorem f(x)=\sqrt{x+2\sqrt{221}}. Wartość funkcji f dla argumentu x=\left(\sqrt{17}-\sqrt{13}\right)^2 jest równa:
Odpowiedzi:
A. \sqrt{223+4\sqrt{221}} B. \sqrt{219}
C. \sqrt{221+4\sqrt{221}} D. \sqrt{30}
Zadanie 11.  1 pkt ⋅ Numer: pp-10745 ⋅ Poprawnie: 165/249 [66%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 Funkcja f przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą.

Spośród liczb: f(50), f(51), f(52), f(54) największa to:

Odpowiedzi:
A. f(54) B. f(50)
C. f(52) D. f(51)
Zadanie 12.  1 pkt ⋅ Numer: pp-10719 ⋅ Poprawnie: 145/188 [77%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 « Funkcja f przyporządkowuje każdej liczbie naturalnej większej od 1 resztę z dzielenia tej liczby przez 23.

Spośród liczb: f(78), f(88), f(103), f(115) największą jest:

Odpowiedzi:
A. f(115) B. f(78)
C. f(88) D. f(103)
Zadanie 13.  1 pkt ⋅ Numer: pp-10714 ⋅ Poprawnie: 295/395 [74%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 Funkcja f każdej liczbie naturalnej ze zbioru \{ 14,18,24,29\} przyporządkowuje resztę z dzielenia tej liczby przez 4.

Zbiorem wartości tej funkcji jest zbiór:

Odpowiedzi:
A. \{0,1,3\} B. \{1,2,3\}
C. \{0,2,3\} D. \{0,1,2\}
Zadanie 14.  1 pkt ⋅ Numer: pp-10717 ⋅ Poprawnie: 187/247 [75%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 Funkcja f przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 7.

Oblicz wartość wyrażenia \frac{f(29)}{f(39)}.

Odpowiedź:
\frac{f(m)}{f(n)}=
(wpisz dwie liczby całkowite)
Zadanie 15.  1 pkt ⋅ Numer: pp-10729 ⋅ Poprawnie: 896/1399 [64%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
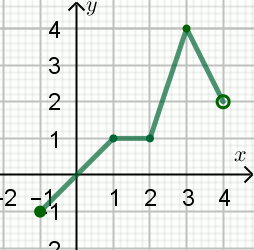
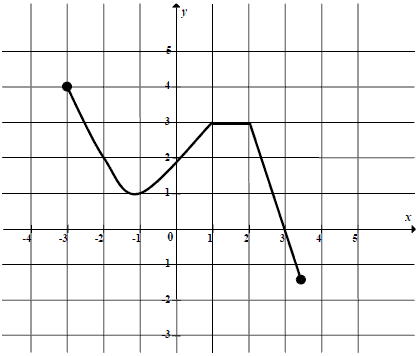
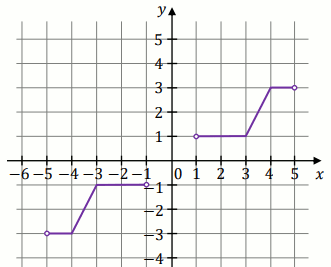
Zbiorem wartości funkcji, której wykres pokazano na rysunku jest:
Odpowiedzi:
A. \langle -1,4\rangle B. \langle -1,4)
C. \langle -1,2)\cup(2,4\rangle D. (-1,4)-\{2\}
Zadanie 16.  1 pkt ⋅ Numer: pp-10728 ⋅ Poprawnie: 472/597 [79%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji y=f(x).

Podaj największą wartość tej funkcji.

Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 17.  1 pkt ⋅ Numer: pp-10727 ⋅ Poprawnie: 508/752 [67%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 « Na rysunku przedstawiono wykres funkcji f:

Zbiorem wartości funkcji g określonej wzorem g(x)=f(x)+3 jest zbiór:

Odpowiedzi:
A. \left\langle -1,\frac{49}{8}\right\rangle B. \left\langle -3,\frac{33}{8}\right\rangle
C. \left\langle -2,\frac{41}{8}\right\rangle D. \left\langle 1,\frac{65}{8}\right\rangle
Zadanie 18.  1 pkt ⋅ Numer: pp-10724 ⋅ Poprawnie: 580/885 [65%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 Na rysunku przedstawiony jest wykres funkcji y=f(x). Rozwiązaniem nierówności f(x)\geqslant 1 jest przedział:
Odpowiedzi:
A. \left\langle -3,6\right\rangle B. \left\langle -\frac{5}{2},0\right\rangle
C. \left\langle -\frac{7}{2},6\right\rangle D. \langle -4,6\rangle
Zadanie 19.  1 pkt ⋅ Numer: pp-10747 ⋅ Poprawnie: 142/211 [67%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
 « Funkcja f opisana jest wzorem: f(x)=2026(-4x+3)^{2026}-1.

Oblicz f(1).

Odpowiedź:
f(x)= (wpisz liczbę całkowitą)
Zadanie 20.  1 pkt ⋅ Numer: pp-10748 ⋅ Poprawnie: 107/128 [83%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 Funkcja f opisana jest wzorem: f(x)=\sqrt[3]{3-4x}.

Wówczas f(x-2) jest równa:

Odpowiedzi:
A. \sqrt[3]{4x+1} B. \sqrt[3]{-4x+11}
C. \sqrt[3]{3-4x}-2 D. \sqrt[3]{-4x+7}
Zadanie 21.  1 pkt ⋅ Numer: pp-10759 ⋅ Poprawnie: 143/221 [64%] Rozwiąż 
Podpunkt 21.1 (1 pkt)
 « Funkcja f przyporządkowuje dowolnej liczbie całkowitej n ostatnią cyfrę 3-ej potęgi liczby n.

Ile elementów należy do zbioru wartości tej funkcji?

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 22.  1 pkt ⋅ Numer: pp-10743 ⋅ Poprawnie: 58/100 [58%] Rozwiąż 
Podpunkt 22.1 (1 pkt)
 « Dziedziną funkcji g(x)=\frac{4x-28}{|7-x|} jest zbiór (7,+\infty).

Zatem:

Odpowiedzi:
A. ZW_{g}=\{4\} B. ZW_{g}=\{-4,4\}
C. ZW_{g}=\mathbb{R}-\{4\} D. ZW_{g}=\mathbb{R}-\{-4\}
Zadanie 23.  1 pkt ⋅ Numer: pp-10740 ⋅ Poprawnie: 100/128 [78%] Rozwiąż 
Podpunkt 23.1 (1 pkt)
 Funkcja f opisana jest wzorem f(x)=\frac{1+11x}{x-1} dla pewnego argumentu przyjmuje wartość \sqrt{122}.

Argumentem tym jest:

Odpowiedzi:
A. \sqrt{122}-1 B. 122+\sqrt{122}
C. \left(\sqrt{122}+1\right)^2 D. \frac{\sqrt{122}+1}{\sqrt{122}-11}
Zadanie 24.  1 pkt ⋅ Numer: pp-10715 ⋅ Poprawnie: 74/96 [77%] Rozwiąż 
Podpunkt 24.1 (1 pkt)
 Funkcja f przyporządkowuje każdej liczbie naturalnej n większej od 1 ilość liczb pierwszych mniejszych od n.

Oblicz f(32)-f(15).

Odpowiedź:
f(x_1)-f(x_2)= (wpisz liczbę całkowitą)
Zadanie 25.  1 pkt ⋅ Numer: pp-10716 ⋅ Poprawnie: 72/134 [53%] Rozwiąż 
Podpunkt 25.1 (1 pkt)
 « Funkcja f, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie n ostatnią cyfrę jej kwadratu, a zbiór wartości funkcji f zawiera k elementów.

Wyznacz k.

Odpowiedź:
k= (wpisz liczbę całkowitą)
Zadanie 26.  1 pkt ⋅ Numer: pp-10764 ⋅ Poprawnie: 599/767 [78%] Rozwiąż 
Podpunkt 26.1 (1 pkt)
Rysunek przedstawia wykres pewnej funkcji y=f(x), określonej dla x\in\langle -4, 4\rangle.

Zbiór wszystkich argumentów, dla których funkcja f przyjmuje wartości niedodatnie, to zbiór:

Odpowiedzi:
A. \langle -4,-3\rangle \cup \langle 0,4\rangle B. \langle 0,3) \cup (3,4\rangle
C. (-4,-3)\cup(0,3)\cup(3,4) D. (-2,1)\cup(3,4)
Zadanie 27.  1 pkt ⋅ Numer: pp-10753 ⋅ Poprawnie: 58/83 [69%] Rozwiąż 
Podpunkt 27.1 (1 pkt)
Wartością funkcji dla argumentu naturalnego n jest ostatnia cyfra kwadratu liczby n zwiększona o 2. Wynika stąd, że zbiór wartości funkcji zawiera liczbę:
Odpowiedzi:
A. 9 B. 4
C. 7 D. 5
Zadanie 28.  1 pkt ⋅ Numer: pp-11390 ⋅ Poprawnie: 169/214 [78%] Rozwiąż 
Podpunkt 28.1 (1 pkt)
 Do zbioru wartości funkcji f(x)=-1-|x|, gdzie x\in\mathbb{N} należy liczba:
Odpowiedzi:
A. \frac{1}{4} B. 5
C. 2 D. -4
Zadanie 29.  1 pkt ⋅ Numer: pp-10711 ⋅ Poprawnie: 215/283 [75%] Rozwiąż 
Podpunkt 29.1 (1 pkt)
 Funkcja f określona jest wzorem f(x)=2\sqrt{x} dla x\in\{1,4,9,16,25,36,49\}.

Do zbioru wartości tej funkcji nie należy liczba:

Odpowiedzi:
A. 7 B. 14
C. 12 D. 8
E. 10 F. 4
Zadanie 30.  1 pkt ⋅ Numer: pp-10760 ⋅ Poprawnie: 61/114 [53%] Rozwiąż 
Podpunkt 30.1 (0.5 pkt)
 Zbiorem wartości funkcji f jest przedział \langle -15,-1\rangle. Wyznacz zbiór tych wartości parametru q, dla których funkcja określona wzorem g(x)=f(x)+q nie ma miejsc zerowych.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.

Odpowiedź:
min= (wpisz liczbę całkowitą)
Podpunkt 30.2 (0.5 pkt)
 Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
max= (wpisz liczbę całkowitą)
Zadanie 31.  1 pkt ⋅ Numer: pp-10710 ⋅ Poprawnie: 93/138 [67%] Rozwiąż 
Podpunkt 31.1 (1 pkt)
 « Funkcja f określona jest wzorem f(x)=\sqrt[3]{x}-\frac{1}{\sqrt[3]{x^2}}.

Wtedy liczba f(-9) jest równa:

Odpowiedzi:
A. -\frac{10}{9}\sqrt[3]{81} B. -\frac{9}{10}\sqrt[3]{9}
C. -\frac{9}{10}\sqrt[3]{81} D. -\frac{10}{9}\sqrt[3]{9}
Zadanie 32.  1 pkt ⋅ Numer: pp-10755 ⋅ Poprawnie: 104/125 [83%] Rozwiąż 
Podpunkt 32.1 (1 pkt)
 » Zbiór wartości funkcji f(x)=7-\frac{7}{x+2} nie zawiera liczby:
Odpowiedzi:
A. 4 B. 8
C. 5 D. 13
E. 7 F. 10
Zadanie 33.  1 pkt ⋅ Numer: pp-10703 ⋅ Poprawnie: 173/248 [69%] Rozwiąż 
Podpunkt 33.1 (1 pkt)
 Dana jest funkcja h(x)=\left(-\frac{1}{3}m+2\right)x+\frac{3}{2}m-1. Funkcja ta dla argumentu 1 przyjmuje wartość -6.

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 34.  1 pkt ⋅ Numer: pp-10705 ⋅ Poprawnie: 545/621 [87%] Rozwiąż 
Podpunkt 34.1 (1 pkt)
 Na rysunku przedstawiono wykres funkcji y=f(x).

Wyznacz największą wartość funkcji f w przedziale \langle -2, 1\rangle.

Odpowiedź:
max= (wpisz liczbę całkowitą)
Zadanie 35.  1 pkt ⋅ Numer: pp-10709 ⋅ Poprawnie: 79/90 [87%] Rozwiąż 
Podpunkt 35.1 (1 pkt)
 Funkcja f określona jest wzorem f(x)=\frac{2x^3}{x^6+3} dla każdej liczby rzeczywistej x.

Oblicz wartość funkcji f\left(-\sqrt[3]{6}\right).

Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 36.  1 pkt ⋅ Numer: pp-10762 ⋅ Poprawnie: 252/301 [83%] Rozwiąż 
Podpunkt 36.1 (1 pkt)
Podaj największą wartość funkcji f, której wykres pokazano na rysunku:
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 37.  1 pkt ⋅ Numer: pp-10756 ⋅ Poprawnie: 48/88 [54%] Rozwiąż 
Podpunkt 37.1 (1 pkt)
 « Funkcja f określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie n ostatnią cyfrę jej czwartej potęgi.

Ile liczb zawiera zbiór wartości funkcji f?

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 38.  1 pkt ⋅ Numer: pp-10763 ⋅ Poprawnie: 118/164 [71%] Rozwiąż 
Podpunkt 38.1 (1 pkt)
 Do wykresu funkcji f(x)=ax+\frac{5}{6} określonej dla x\neq -1 należy punkt A=(-2,3).

Wyznacz wartość parametru a.

Odpowiedź:
\frac{m}{n}=
(wpisz dwie liczby całkowite)
Zadanie 39.  1 pkt ⋅ Numer: pp-11810 ⋅ Poprawnie: 828/878 [94%] Rozwiąż 
Podpunkt 39.1 (1 pkt)
 Funkcja f jest określona dla każdej liczby rzeczywistej x wzorem f(x)=\frac{3x-k}{x^2+5} gdzie k jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek f(1)=2.

Wartość współczynnika k we wzorze tej funkcji jest równa:

Odpowiedzi:
A. -9 B. -10
C. -8 D. -11
E. -4 F. -16
G. -3 H. -7
Zadanie 40.  1 pkt ⋅ Numer: pp-11857 ⋅ Poprawnie: 511/564 [90%] Rozwiąż 
Podpunkt 40.1 (1 pkt)
 Na rysunku przedstawiono wykres funkcji f:
Iloczyn f(3)\cdot f(-5)\cdot f(-6) jest równy:
Odpowiedzi:
A. 42 B. 36
C. 31 D. 38
E. 34 F. 39
Zadanie 41.  1 pkt ⋅ Numer: pp-11886 ⋅ Poprawnie: 372/341 [109%] Rozwiąż 
Podpunkt 41.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=\frac{4}{x}-4 dla każdej liczby rzeczywistej x\neq 0.

Liczba f(3)-f(-3) jest równa:

Odpowiedzi:
A. \frac{19}{6} B. \frac{29}{12}
C. \frac{8}{3} D. \frac{2}{3}
E. \frac{5}{3} F. \frac{13}{6}
Zadanie 42.  1 pkt ⋅ Numer: pp-11888 ⋅ Poprawnie: 246/364 [67%] Rozwiąż 
Podpunkt 42.1 (1 pkt)
 Na rysunku jest przedstawiony fragment wykresu funkcji okreslonej wzorem y=f(x):

W przedziale (-4,6) równanie f(x)=-2:

Odpowiedzi:
A. ma trzy rozwiązania B. nie ma rozwiązań
C. ma jedno rozwiązanie D. ma dwa rozwiązania
Zadanie 43.  1 pkt ⋅ Numer: pp-11934 ⋅ Poprawnie: 145/193 [75%] Rozwiąż 
Podpunkt 43.1 (1 pkt)
 Punkt A=(1,2) należy do wykresu funkcji f, określonej wzorem f(x)=(m^2-2m-2)x^3-m^2+3m-1 dla każdej liczby rzeczywistej x.

Wtedy liczba m jest równa:

Odpowiedzi:
A. 6 B. 0
C. 1 D. 2
E. 8 F. 5
Zadanie 44.  1 pkt ⋅ Numer: pp-11961 ⋅ Poprawnie: 245/248 [98%] Rozwiąż 
Podpunkt 44.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=-\log{x}, dla wszystkich liczb rzeczywistych dodatnich x.

Wartość funkcji f dla argumentu x=\sqrt[5]{10^{7}} jest równa:

Odpowiedzi:
A. -\frac{7}{10} B. -\frac{14}{5}
C. \frac{14}{5} D. -\frac{7}{5}
E. \frac{7}{5} F. -\frac{5}{7}
Zadanie 45.  1 pkt ⋅ Numer: pp-12033 ⋅ Poprawnie: 320/269 [118%] Rozwiąż 
Podpunkt 45.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=\frac{3x+5}{4x^2+1} dla każdej liczby rzeczywistej x.

Wartość funkcji f dla argumentu 1 jest równa:

Odpowiedzi:
A. \frac{8}{5} B. \frac{16}{5}
C. 2 D. \frac{4}{5}
E. \frac{32}{25} F. \frac{12}{5}
Zadanie 46.  1 pkt ⋅ Numer: pp-12061 ⋅ Poprawnie: 250/237 [105%] Rozwiąż 
Podpunkt 46.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=\frac{(x+6)^2}{2x+10} dla każdej liczby rzeczywistej x\neq 1.

Wtedy dla argumentu x=\sqrt{3}-7 wartość funkcji f jest równa:

Odpowiedzi:
A. \frac{1}{\sqrt{3}+4} B. \frac{1}{\sqrt{3}}
C. 1 D. \frac{1}{\sqrt{3}+5}
E. -1 F. \sqrt{3}+6
Zadanie 47.  1 pkt ⋅ Numer: pp-12062 ⋅ Poprawnie: 257/237 [108%] Rozwiąż 
Podpunkt 47.1 (1 pkt)
 Do wykresu funkcji f określonej dla każdej liczby rzeczywistej x wzorem f(x)=3^x-5 należy punkt o współrzędnych:
Odpowiedzi:
A. (4,74) B. (2,1)
C. (4,79) D. (1,-3)
E. (0,-5) F. (3,22)
Zadanie 48.  2 pkt ⋅ Numer: pp-20773 ⋅ Poprawnie: 93/227 [40%] Rozwiąż 
Podpunkt 48.1 (1 pkt)
 « Dana jest funkcja f(x)=\frac{1}{x}, gdzie x\in\left(-\frac{8}{5}, -\frac{3}{13}\right).

Podaj najmniejszą liczbę całkowitą, która należy do zbioru wartości tej funkcji.

Odpowiedź:
min_{\in\mathbb{Z},\in ZW_f}= (wpisz liczbę całkowitą)
Podpunkt 48.2 (1 pkt)
 Podaj największą liczbę całkowitą, która należy do zbioru wartości tej funkcji.
Odpowiedź:
max_{\in\mathbb{Z},\in ZW_f }= (wpisz liczbę całkowitą)
Zadanie 49.  3 pkt ⋅ Numer: pp-21052 ⋅ Poprawnie: 133/1094 [12%] Rozwiąż 
Podpunkt 49.1 (1 pkt)
 Dana jest funkcja y=f(x), której wykres pokazano na rysunku:

Dziedziną funkcji f jest zbiór:

Odpowiedzi:
A. [-5,-1]\cup[1,5] B. [-3,-1]\cup[1,3]
C. (-3,-1)\cup(1,3) D. (-5,5)
E. (-3,3) F. (-5,-1)\cup(1,5)
Podpunkt 49.2 (1 pkt)
 Zbiorem wartości funkcji f jest zbiór:
Odpowiedzi:
A. [-5,-1]\cup[1,5] B. (-3,3)
C. (-5,5) D. (-5,-1)\cup(1,5)
E. [-3,-1]\cup[1,3] F. (-3,-1)\cup(1,3)
Podpunkt 49.3 (1 pkt)
 Zbiór A jest zbiorem wszystkich rozwiązań nierówności f(x)\lessdot -1.

Podaj najmniejszą i największą liczbę całkowitą należącą do zbioru A.

Odpowiedzi:
min= (wpisz liczbę całkowitą)
max= (wpisz liczbę całkowitą)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm