⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Monotoniczność funkcji
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- funkcje monotoniczne
- funkcja rosnąca i niemalejąca
- funkcja malejąca i nierosnąca
- funkcja stała
- badanie monotoniczności funkcji
| Zadanie 1. 1 pkt ⋅ Numer: pp-10744 ⋅ Poprawnie: 184/392 [46%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Funkcja f opisana jest wzorem:
f(x)=x^2.
Wówczas:
Odpowiedzi:
| T/N : f\left(3\sqrt{3}\right)=9\sqrt{3} | T/N : f\left(-4\sqrt{3}\right)=-48 |
| T/N : iloczyn x\cdot f(x) jest liczba dodatnią | T/N : funkcja ta jest monotoniczna |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10699 ⋅ Poprawnie: 709/1322 [53%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji f.
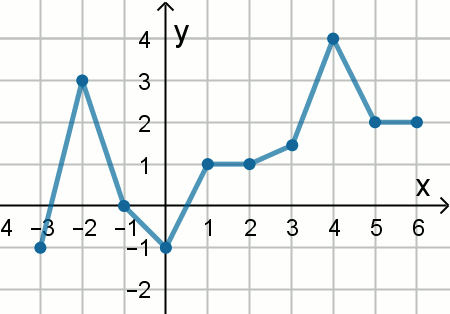
Jaką długość ma najdłuższy przedział, w którym funkcja f jest rosnąca?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10700 ⋅ Poprawnie: 508/905 [56%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji h:
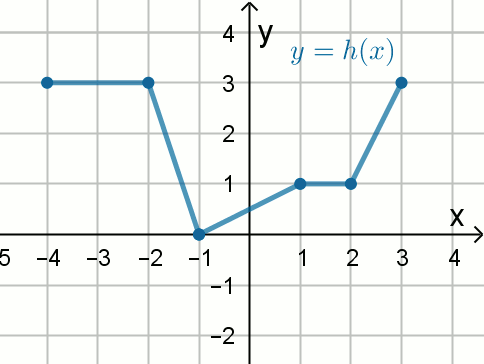
Jaką długość ma najdłuższy przedział, w którym funkcja h niemalejąca?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10698 ⋅ Poprawnie: 205/563 [36%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
«« Dziedziną funkcji f jest przedział
\langle -5,4\rangle:
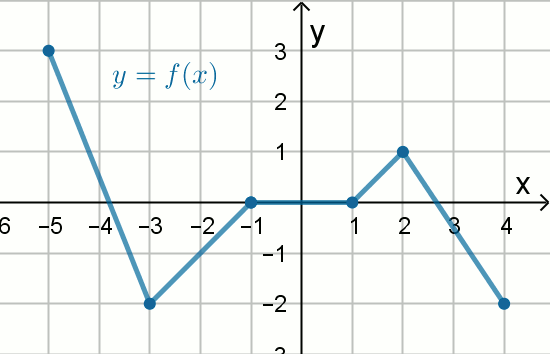
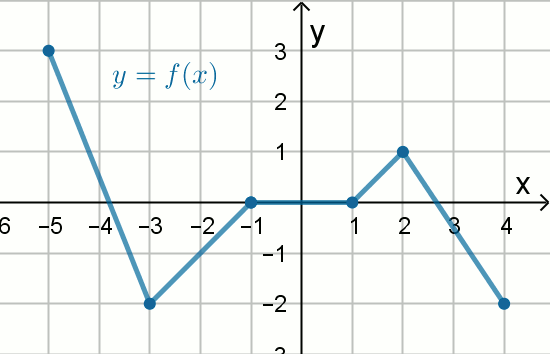
Jaką długość ma najdłuższy przedział, w którym funkcja f jest malejąca?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-11533 ⋅ Poprawnie: 92/471 [19%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
(1 pkt)
Na rysunku pokazano wykres funkcji określonej wzorem y=f(x):
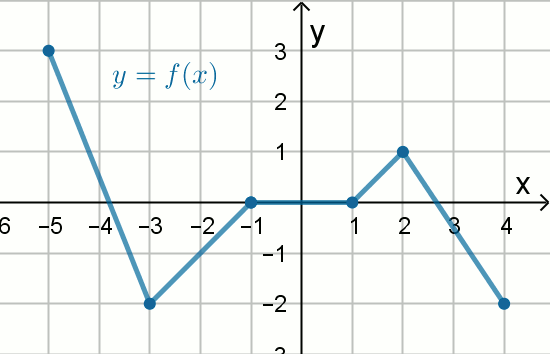
Wskaż zdanie fałszywe:
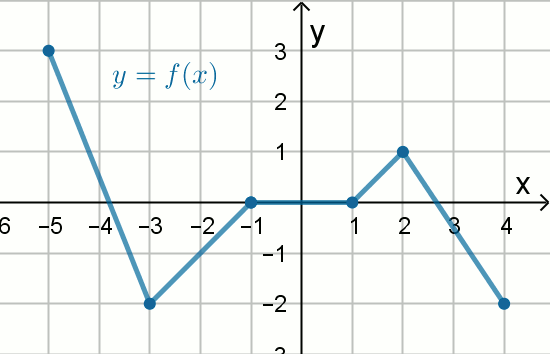
Odpowiedzi:
| A. funkcja f ma ujemne miejsce zerowe | B. ZW_{f}=\langle -2, 3\rangle |
| C. D_{f}=\langle -5, 4\rangle | D. funkcja jest rosnąca w co najmniej dwóch rozłącznych przedziałach |
| E. funkcja jest malejąca, gdy x\in\langle -5, -3\rangle\cup\langle 2, 4\rangle | F. funkcja f nie jest różnowartościowa |
| Zadanie 6. 1 pkt ⋅ Numer: pp-12032 ⋅ Poprawnie: 93/186 [50%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Na wykresie przedstawiono wykres funkcji f:
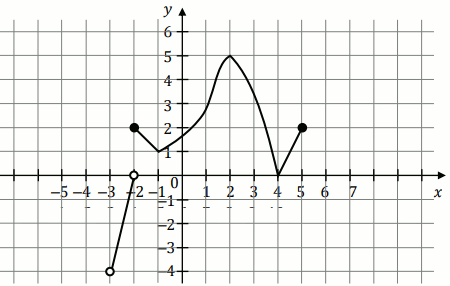
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : dziedziną funkcji f jest przedzial (-4, 5) | T/N : zbiorem wartości funkcji f jest przedział (-4, 5\rangle |
| Zadanie 7. 1 pkt ⋅ Numer: pp-12088 ⋅ Poprawnie: 45/142 [31%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Na poniższym rysunku przedstawiono wykres funkcji f określonej w zbiorze
(-1,7).
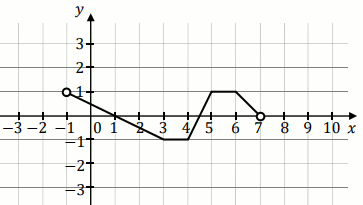
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja f osiąga wartość największą równą 1 | T/N : funkcja f jest monotoniczna w przedziale (-1,4) |
| T/N : zbiorem wartości funkcji f jest przedział [-1,1) |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20292 ⋅ Poprawnie: 254/946 [26%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji f.
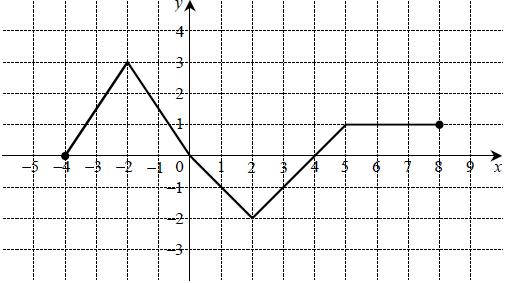
Ile liczb całkowitych należy do zbioru wartości tej funkcji?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Jaką długość ma przedział o maksymalnej długości, w którym funkcja ta jest monotoniczna?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 9. 3 pkt ⋅ Numer: pp-21044 ⋅ Poprawnie: 713/1026 [69%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji określonej wzorem y=f(x):
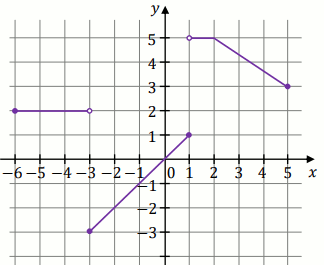
Dziedziną tej funkcji jest zbiór:
Odpowiedzi:
| A. [-3,5] | B. (-6,5) |
| C. [-3,5) | D. [-6,5] |
Podpunkt 9.2 (1 pkt)
Największa wartość tej funkcji w przedziale [-5,1]
jest równa:
Odpowiedzi:
| A. 2 | B. 5 |
| C. 3 | D. 1 |
Podpunkt 9.3 (1 pkt)
Funkcja f jest malejąca w zbiorze:
Odpowiedzi:
| A. [-6,-3] | B. (1,2] |
| C. [2,5] | D. [-3,1] |