⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Dwie proste przecięte trzecią prostą. Suma kątów w trójkącie.
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- kąty w trójkącie
- kąty naprzemianległe
- kąty odpowiadające
| Zadanie 1. 2 pkt ⋅ Numer: pp-20239 ⋅ Poprawnie: 322/471 [68%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch
pozostałych kątów, których miary różnią się o 30^{\circ}.
Oblicz miarę najmniejszego kąta tego trójkąta.
Odpowiedź:
| \beta_{min}= | |
Podpunkt 1.2 (1 pkt)
Oblicz miarę największego kąta tego trójkąta.
Odpowiedź:
| \beta_{max}= | |
| Zadanie 2. 2 pkt ⋅ Numer: pp-20200 ⋅ Poprawnie: 60/116 [51%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Czworokąt ABCD jest kwadratem, a zielone trójkąty
są równoboczne:
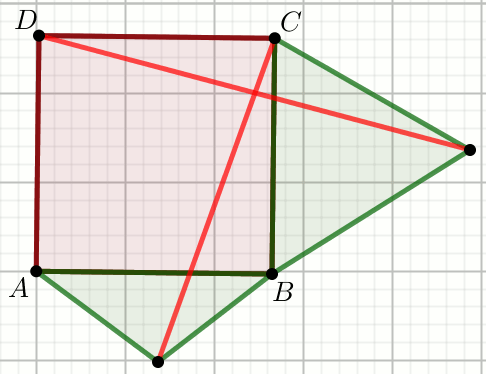
Podaj miarę najmniejszego kąta między czerwonymi odcinkami.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 3. 2 pkt ⋅ Numer: pp-20853 ⋅ Poprawnie: 55/757 [7%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
(2 pkt)
« W trójkącie równoramiennym ABC o podstawie
AB, wysokość AD
tworzy z jego podstawą kąt o mierze
\alpha i dzieli kąt wewnętrzny tego trójkąta przy wierzchołku
A w stosunku 1:k.
Wiedząc, że liczby k i \alpha
są naturalne dodatnie wykaż, że miara kąta \alpha
jest dzielnikiem liczby 90.
Wyznacz największą możliwą wartość k.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. 2 pkt ⋅ Numer: pp-20876 ⋅ Poprawnie: 10/22 [45%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Trzy liczby x+1, +5-x i
4x+8 są długościami boków trójkąta, gdy liczba liczba
x należy do przedziału (p,q).
Podaj liczbę p.
Odpowiedź:
| p= | |
Podpunkt 4.2 (1 pkt)
Podaj liczbę q.
Odpowiedź:
| q= | |
| Zadanie 5. 2 pkt ⋅ Numer: pp-20877 ⋅ Poprawnie: 15/24 [62%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
Trzy liczby 2x-9, x-1 i
4x-29 są długościami boków trójkąta równoramiennego.
Wyznacz najmniejszy możliwy L_{min} i największy możliwy L_{max} obwód tego trójkąta.
Odpowiedzi:
| L_{min} | = |
(wpisz liczbę całkowitą) |
| L_{max} | = |
(wpisz liczbę całkowitą) |