Suma kątów w trójkącie
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- suma kątów w trójkącie
- nierówność trójkąta
- odcinek łączący środki boków trójkąta
| Zadanie 1. 1 pkt ⋅ Numer: pp-10575 ⋅ Poprawnie: 362/475 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Kąty trójkąta mają miary \alpha,\beta,\gamma.
Wiadomo, że \beta=3\cdot \alpha oraz
\gamma=2\cdot \alpha.
Trójkąt ten jest:
Odpowiedzi:
| A. ostrokątny | B. równoramienny |
| C. prostokątny | D. rozwartokątny |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11564 ⋅ Poprawnie: 114/140 [81%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W trójkącie różnobocznym dwa boki mają długości odpowiednio 14 i
18, a długość trzeciego boku leżącego naprzeciwko najmniejszego
kąta w tym trójkącie jest liczbą całkowitą.
Wyznacz najmniejszą możliwą i największą możliwą długość trzeciego boku tego trójkąta.
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11563 ⋅ Poprawnie: 33/88 [37%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
«« W trójkącie różnobocznym dwa najkrótsze boki mają długość 11 i
18, a długość trzeciego boku jest liczbą całkowitą.
Wyznacz najmniejszą możliwą i największą możliwą długość najdłuższego boku tego trójkąta.
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10582 ⋅ Poprawnie: 115/137 [83%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Z odcinków o długościach: 13,
x-1, 2x+3,
5x+3 można zbudować trapez równoramienny.
Wyznacz najmniejsze możliwe x.
Odpowiedź:
| x_{min}= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11562 ⋅ Poprawnie: 59/139 [42%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
W trójkącie ABC połączono środki
trzech boków i otrzymano trójkąt PQR o obwodzie o
\frac{20}{3} mniejszym od obwodu trójkąta ABC.
Oblicz obwód trójkąta ABC.
Odpowiedź:
| L_{ABC}= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10659 ⋅ Poprawnie: 346/433 [79%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
W trapezie ABCD boki AD
i CD mają taką samą długość, a kąt
\beta ma miarę 98^{\circ}:
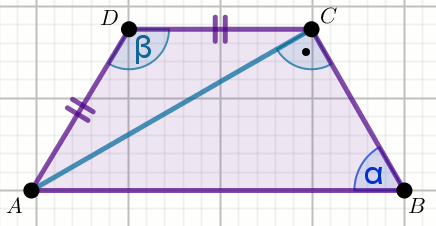

Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 7. 1 pkt ⋅ Numer: pp-10580 ⋅ Poprawnie: 240/318 [75%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Oblicz obwód trójkąta równobocznego o polu powierzchni równym 6\sqrt{3}.
Odpowiedź:
m\sqrt{n}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 8. 1 pkt ⋅ Numer: pp-10579 ⋅ Poprawnie: 248/239 [103%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Z prostokąta ABCD o obwodzie
30 wycięto trójkąt równoboczny
AOD o obwodzie 15
(tak jak na rysunku).
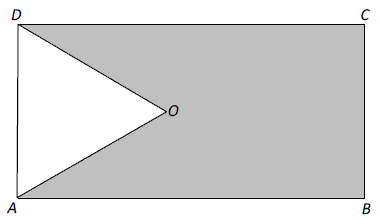

Obwód zacieniowanej figury jest równy:
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 9. 1 pkt ⋅ Numer: pp-11497 ⋅ Poprawnie: 204/210 [97%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
W trapezie ABCD boki AD
i CD mają taką samą długość, a kąt
\alpha ma miarę 75^{\circ}:


Oblicz miarę stopniową kąta \beta.
Odpowiedź:
\beta\ [^{\circ}]=
(wpisz liczbę całkowitą)
| Zadanie 10. 1 pkt ⋅ Numer: pp-11561 ⋅ Poprawnie: 134/109 [122%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« W trójkącie o obwodzie długości 20 połączono środki
trzech boków i otrzymano trójkąt.
Oblicz obwód otrzymanego trójkąta.
Odpowiedź:
| L= | |
| Zadanie 11. 1 pkt ⋅ Numer: pp-11895 ⋅ Poprawnie: 118/144 [81%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
W trójkącie miary kątów są równe: \alpha+2^{\circ},
4\alpha+8^{\circ}, \alpha+32^{\circ}.
Miara największego kąta tego trójkąta jest równa:
Odpowiedzi:
| A. 95^{\circ} | B. 96^{\circ} |
| C. 100^{\circ} | D. 97^{\circ} |
| E. 99^{\circ} | F. 98^{\circ} |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11896 ⋅ Poprawnie: 218/210 [103%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Na boku BC kwadratu ABCD (na zewnątrz) zbudowano
trójkąt równoboczny BEC (zobacz rysunek).
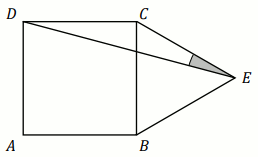

Miara kąta DEC jest równa:
Odpowiedzi:
| A. 15^{\circ} | B. 20^{\circ} |
| C. 24^{\circ} | D. 18^{\circ} |
| E. 12^{\circ} | F. 10^{\circ} |
| Zadanie 13. 1 pkt ⋅ Numer: pp-12096 ⋅ Poprawnie: 12/38 [31%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Jeden z boków równoległoboku ma długość równą 35.
Przekątne tego równoległoboku mogą mieć długości:
Odpowiedzi:
| A. 28 i 42 | B. 70 i 70 |
| C. 35 i 35 | D. 28 i 21 |