⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Trójkąty podobne
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- podobieństwo trójkątów
- cechy podobieństwa trójkątów
| Zadanie 1. 2 pkt ⋅ Numer: pr-20025 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Wysokość prostokąta wpisanego w trójkąt o podstawie długości
6 ma długość h:
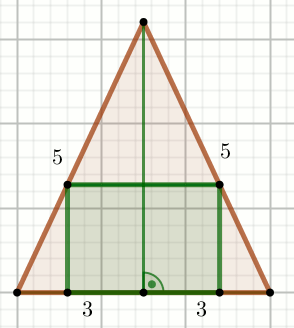
Oblicz pole powierzchni tego prostokąta.
Dane
h=3.00
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Oblicz obwód tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20752 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Dany jest trójkąt:
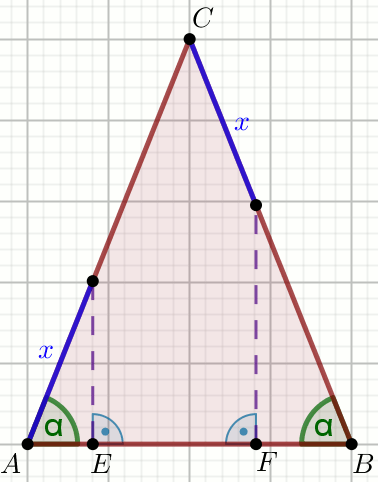
Oblicz \frac{|EF|}{|AB|}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20882 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
«« W prostokącie ABCD punkt M należy do boku
CD i jest tak położony, że AM\perp BD.
Przekątna BD przecina odcinek AM
w punkcie N oraz |AN|=27 i
|NM|=3.
Oblicz długość przekątnej AC.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (1 pkt)
Oblicz obwód tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 3 pkt ⋅ Numer: pr-21198 ⋅ Poprawnie: 2/8 [25%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Dany jest trójkąt równoramienny ABC, w którym
|AC|=|AB|=21, a punkt D jest środkiem podstawy
AB. Okrąg o środku D jest styczny do prostej
AC w punkcie M. Punkt K
leży na boku AC, punkt L leży na boku
BC, odcinek KL jest styczny do rozważanego okręgu
oraz |KC|=|LC|=3 (zobacz rysunek).
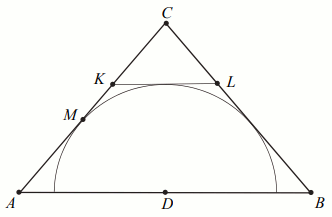
Oblicz |KL|.
Odpowiedź:
| |KL|= | |
Podpunkt 4.2 (2 pkt)
Oblicz \frac{|AM|}{|MC|}.
Odpowiedź:
| |AM|:|MC|= | |