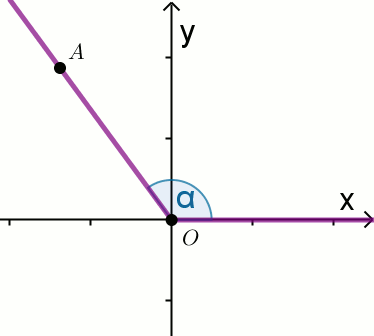Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Funkcje trygonometryczne

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10638 ⋅ Poprawnie: 1020/1641 [62%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 Kąt \alpha jest kątem ostrym w trójkącie prostokątnym. Przeciwprostokątna tego trójkąta ma długość 12, a \cos\alpha=\frac{1}{6}.

Wynika z tego, że:

Odpowiedzi:
A. jedna z przyprostokątnych jest 6 razy krótsza od przeciwprostokątnej B. przyprostokatna tego trójkąta ma długość 1
C. przeciwprostokątna tego trójkąta jest dwa razy dłuższa od przyprostokątnej D. \sin\alpha=\frac{5}{6}
Zadanie 2.  1 pkt ⋅ Numer: pp-10627 ⋅ Poprawnie: 444/634 [70%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Kąt \alpha spełnia warunki: \alpha\in(0^{\circ},90^{\circ}) i \tan\alpha=\frac{48}{55}.

Oblicz \sin\alpha.

Odpowiedź:
\sin\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 3.  1 pkt ⋅ Numer: pp-10632 ⋅ Poprawnie: 841/1003 [83%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 Kąt \alpha jest ostry i \cos\alpha=\frac{55}{73}.

Oblicz \sin\alpha.

Odpowiedź:
\sin\alpha=
(wpisz dwie liczby całkowite)
Zadanie 4.  1 pkt ⋅ Numer: pp-10626 ⋅ Poprawnie: 178/286 [62%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 Kąty ostre \alpha i \beta trójkąta prostokątnego spełniają warunek \frac{\sin \alpha}{\sin\beta}=\frac{\sqrt{11}}{11}. Oblicz \cos\alpha i zapisz wynik w najprostszej nieskracalnej postaci \frac{a\sqrt{b}}{c}.

Podaj liczby a, b i c.

Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-10631 ⋅ Poprawnie: 374/652 [57%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 Wiadomo, że kąt \alpha jest ostry oraz \sin\alpha=\frac{6\sqrt{37}}{37}.

Oblicz wartość wyrażenia \sin \alpha-\cos\alpha.

Odpowiedź:
\sin\alpha-\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 6.  1 pkt ⋅ Numer: pp-10640 ⋅ Poprawnie: 622/839 [74%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 Wiadomo, że kąt \alpha jest ostry oraz \tan\alpha=6.

Oblicz \sin\alpha.

Odpowiedź:
\sin\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 7.  1 pkt ⋅ Numer: pp-10641 ⋅ Poprawnie: 523/739 [70%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 Wiadomo, że kąt \alpha jest ostry oraz. \sin\alpha=\frac{4\sqrt{17}}{17}.

Oblicz \cos\alpha.

Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 8.  1 pkt ⋅ Numer: pp-10613 ⋅ Poprawnie: 435/649 [67%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 « Wiadomo, że kąt \alpha jest ostry oraz \tan\alpha=\frac{5}{7}.

Oblicz wartość wyrażenia \sin\alpha+\cos\alpha.

Odpowiedź:
\sin\alpha+\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 9.  1 pkt ⋅ Numer: pp-10617 ⋅ Poprawnie: 402/567 [70%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Wiadomo, że kąt \alpha jest ostry oraz \sin\alpha=\frac{7\sqrt{53}}{53}.

Oblicz wartość wyrażenia 1+\tan\alpha\cdot\cos\alpha.

Odpowiedź:
1+\tan\alpha\cdot\cos\alpha= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 10.  1 pkt ⋅ Numer: pp-10614 ⋅ Poprawnie: 689/1065 [64%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 « Kąt \alpha jest kątem ostrym oraz \tan\alpha=\frac{9}{2}.

Oblicz wartość wyrażenia w=\frac{3\cos\alpha-2\sin\alpha}{\sin\alpha-5\cos\alpha}.

Odpowiedź:
w=
(wpisz dwie liczby całkowite)
Zadanie 11.  1 pkt ⋅ Numer: pp-10621 ⋅ Poprawnie: 316/544 [58%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 Wiadomo, że \alpha=43^{\circ} oraz \cos\alpha=x.

Zatem \cos 47^{\circ} jest równe:

Odpowiedzi:
A. 1-x B. \sqrt{1-x^2}
C. 1-x^2 D. 1+x^2
Zadanie 12.  1 pkt ⋅ Numer: pp-10624 ⋅ Poprawnie: 268/420 [63%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
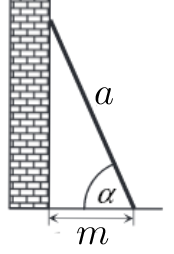
 Pod jakim kątem \alpha padają na powierzchnię Ziemi promienie słoneczne, jeśli długość cienia stojącego człowieka jest 5 razy mniejsza od jego wzrostu?

Oblicz miarę stopniową kąta \alpha. Podaj wynik zaokrąglony do całych stopni.

Odpowiedź:
\alpha\ [^{\circ}]= (wpisz liczbę całkowitą)
Zadanie 13.  1 pkt ⋅ Numer: pp-10637 ⋅ Poprawnie: 846/1248 [67%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 Drabinę o długości 3 metrów oparto o pionowy mur, a jej podstawę umieszczono w odległości 2 metrów od tego muru.

Kąt \alpha, pod jakim ustawiono drabinę, spełnia warunek:

Odpowiedzi:
A. 45^{\circ}\lessdot \alpha&\lessdot60^{\circ} B. 60^{\circ}\lessdot \alpha&\lessdot90^{\circ}
C. 0^{\circ}\lessdot \alpha&\lessdot30^{\circ} D. 30^{\circ}\lessdot \alpha&\lessdot45^{\circ}
Zadanie 14.  1 pkt ⋅ Numer: pp-10620 ⋅ Poprawnie: 478/671 [71%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 Kąt \alpha jest kątem ostrym i \tan \alpha=\frac{11}{13}.

Wówczas:

Odpowiedzi:
A. \alpha\in(42^{\circ},48^{\circ}) B. \alpha\in(38^{\circ},42^{\circ})
C. \alpha\in(34^{\circ},38^{\circ}) D. \alpha\in(48^{\circ},52^{\circ})
Zadanie 15.  1 pkt ⋅ Numer: pp-10609 ⋅ Poprawnie: 609/829 [73%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
 Kąt \alpha jest ostry i \sin \alpha=\frac{1}{9}.

Wówczas:

Odpowiedzi:
A. \cos\alpha=\frac{\sqrt{79}}{9} B. \cos\alpha \lessdot \frac{\sqrt{79}}{9}
C. \cos\alpha > \frac{\sqrt{79}}{9} D. \cos\alpha=\frac{\sqrt{82}}{9}
Zadanie 16.  1 pkt ⋅ Numer: pp-10672 ⋅ Poprawnie: 470/668 [70%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
 « Przeciwprostokątna trójkąta ma długość 18, zaś \alpha jest jednym z dwóch kątów ostrych tego trójkąta i \sin\alpha=\frac{\sqrt{2}}{6}.

Oblicz długość a przyprostokątnej przyległej do kąta \alpha.

Odpowiedź:
a= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 17.  1 pkt ⋅ Numer: pp-10671 ⋅ Poprawnie: 260/413 [62%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 « W trójkącie prostokątnym przyprostokątne mają długość 4\sqrt{3} i 7.

Oblicz cosinus tego kąta ostrego, którego cosinus jest mniejszy.

Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 18.  1 pkt ⋅ Numer: pp-10670 ⋅ Poprawnie: 325/571 [56%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
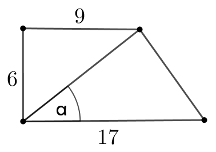
 « Trapez na rysunku jest prostokątny:

Miara kąta \alpha spełnia warunek:

Odpowiedzi:
A. \alpha=45^{\circ} B. 50^{\circ} \lessdot \alpha < 60^{\circ}
C. \alpha=30^{\circ} D. 30^{\circ} \lessdot \alpha < 35^{\circ}
Zadanie 19.  1 pkt ⋅ Numer: pp-10665 ⋅ Poprawnie: 120/181 [66%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
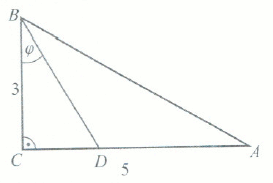
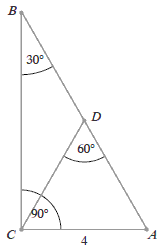
 « Odcinek BD jest dwusieczną kąta na rysunku:

Miara kąta \varphi spełnia warunek:

Odpowiedzi:
A. 25^{\circ} \lessdot \varphi < 30^{\circ} B. 20^{\circ} \lessdot \varphi < 25^{\circ}
C. 30^{\circ} \lessdot \varphi < 35^{\circ} D. 35^{\circ} \lessdot \varphi < 40^{\circ}
Zadanie 20.  1 pkt ⋅ Numer: pp-10663 ⋅ Poprawnie: 407/671 [60%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 » Trójkąt ABC jest prostokątny, a kąt BCA jest prosty. Wiadomo, że \cos\sphericalangle CAB=\frac{45}{53} i |AB|=\frac{53}{2}.

Oblicz długość boku BC.

Odpowiedź:
|BC|=
(wpisz dwie liczby całkowite)
Zadanie 21.  1 pkt ⋅ Numer: pp-10661 ⋅ Poprawnie: 340/461 [73%] Rozwiąż 
Podpunkt 21.1 (1 pkt)
 Przeciwprostokątna AB trójkąta ABC ma długość 29, a \cos \sphericalangle B=\frac{21}{29}.

Oblicz długość przyprostokątnej BC tego trójkąta.

Odpowiedź:
|BC|=
(wpisz dwie liczby całkowite)
Zadanie 22.  1 pkt ⋅ Numer: pp-10658 ⋅ Poprawnie: 119/184 [64%] Rozwiąż 
Podpunkt 22.1 (1 pkt)
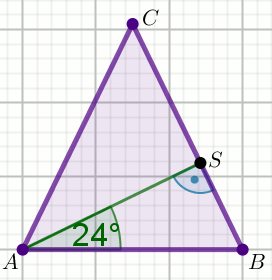
 » W trójkącie równoramiennym ABC poprowadzono wysokość AS, która utworzyła z podstawą kąt o mierze 24^{\circ} (zobacz rysunek).

Ramię tego trójkąta ma długość 10. Długość wysokości AS jest liczbą z przedziału:

Odpowiedzi:
A. \left(\frac{13}{2}, \frac{15}{2}\right\rangle B. \left\langle\frac{7}{2}, \frac{9}{2}\right\rangle
C. \left(\frac{15}{2}, \frac{17}{2}\right\rangle D. \left\langle\frac{11}{2}, \frac{13}{2}\right\rangle
Zadanie 23.  1 pkt ⋅ Numer: pp-10653 ⋅ Poprawnie: 733/897 [81%] Rozwiąż 
Podpunkt 23.1 (1 pkt)
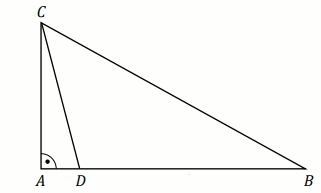
 Dany jest trójkąt:

Oblicz długość odcinka BD.

Odpowiedź:
|BD|= (wpisz liczbę całkowitą)
Zadanie 24.  1 pkt ⋅ Numer: pp-10652 ⋅ Poprawnie: 493/638 [77%] Rozwiąż 
Podpunkt 24.1 (1 pkt)
 W trójkącie prostokątnym długość jednej z przyprostokątnych jest równa 9, zaś długość przeciwprostokątnej jest równa 11.

Oblicz tangens mniejszego kąta ostrego w tym trójkącie.

Odpowiedź:
\tan\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 25.  1 pkt ⋅ Numer: pp-10651 ⋅ Poprawnie: 346/498 [69%] Rozwiąż 
Podpunkt 25.1 (1 pkt)
 W trapezie prostokątnym kąt ostry ma miarę 45^{\circ}, a podstawy mają długości 10 i 13.

Oblicz długość wysokości tego trapezu.

Odpowiedź:
h= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 26.  1 pkt ⋅ Numer: pp-10648 ⋅ Poprawnie: 357/571 [62%] Rozwiąż 
Podpunkt 26.1 (1 pkt)
 « Oblicz długość wysokości trapezu równoramiennego o kącie ostrym 30^{\circ} i ramieniu długości 4\sqrt{7}.
Odpowiedź:
h= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 27.  1 pkt ⋅ Numer: pp-10650 ⋅ Poprawnie: 282/395 [71%] Rozwiąż 
Podpunkt 27.1 (1 pkt)
 Oblicz tangens najmiejszego kąta w trójkącie prostokątnym o bokach długości 14, \frac{45}{2}, \frac{53}{2}.
Odpowiedź:
\tan\alpha=
(wpisz dwie liczby całkowite)
Zadanie 28.  1 pkt ⋅ Numer: pp-10649 ⋅ Poprawnie: 294/493 [59%] Rozwiąż 
Podpunkt 28.1 (1 pkt)
 « W trójkącie prostokątnym najdłuższy bok ma długość 58, a najkrótszy 40.

Oblicz tangens największego kąta ostrego tego trójkąta.

Odpowiedź:
\tan\alpha=
(wpisz dwie liczby całkowite)
Zadanie 29.  1 pkt ⋅ Numer: pp-10680 ⋅ Poprawnie: 167/250 [66%] Rozwiąż 
Podpunkt 29.1 (1 pkt)
 « Oblicz sinus kąta ostrego utworzonego w trójkącie prostokątnym przez boki o długościach 4 i 5.
Odpowiedź:
\sin\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 30.  1 pkt ⋅ Numer: pp-10646 ⋅ Poprawnie: 149/281 [53%] Rozwiąż 
Podpunkt 30.1 (1 pkt)
 « Na płaszczyźnie dane są punkty A=\left(7\sqrt{6},21\sqrt{2}\right), B=\left(0,0\right) i C=\left(7\sqrt{6},0\right).

Kąt CBA ma miarę:

Odpowiedzi:
A. 75^{\circ} B. 30^{\circ}
C. 45^{\circ} D. 60^{\circ}
Zadanie 31.  1 pkt ⋅ Numer: pp-10676 ⋅ Poprawnie: 261/358 [72%] Rozwiąż 
Podpunkt 31.1 (1 pkt)
 « Dany jest trójkąt prostokątny o kątach ostrych \alpha i \beta, w którym \sin\alpha=\frac{2}{3}.

Oblicz \cot \beta.

Odpowiedź:
\cot\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 32.  1 pkt ⋅ Numer: pp-10677 ⋅ Poprawnie: 78/124 [62%] Rozwiąż 
Podpunkt 32.1 (1 pkt)
 W trójkącie prostokątnym przyprostokątne mają długości 4 i 5.

Oblicz cosinus większego z kątów ostrych tego trójkąta.

Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 33.  1 pkt ⋅ Numer: pp-10645 ⋅ Poprawnie: 468/600 [78%] Rozwiąż 
Podpunkt 33.1 (1 pkt)
 » Dane są długości boków |BC|=5 i |AC|=4 trójkąta prostokątnego ABC o kącie ostrym \beta.

Oblicz x=\cos\beta.

Odpowiedź:
x= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 34.  1 pkt ⋅ Numer: pp-11539 ⋅ Poprawnie: 345/416 [82%] Rozwiąż 
Podpunkt 34.1 (1 pkt)
 Punkt A zaznaczony na rysunku ma współrzędne A=(-4,7):
Oblicz tangens kąta \alpha zaznaczonego na rysunku.
Odpowiedź:
\tan\alpha=
(wpisz dwie liczby całkowite)
Zadanie 35.  1 pkt ⋅ Numer: pp-11840 ⋅ Poprawnie: 462/657 [70%] Rozwiąż 
Podpunkt 35.1 (1 pkt)
 Kąt \alpha jest ostry oraz \sin\alpha=\frac{3\sqrt{10}}{10}.

Tangens kąta \alpha jest równy:

Odpowiedzi:
A. \sqrt{10} B. \frac{\sqrt{10}}{10}
C. 3 D. \frac{1}{3}
Zadanie 36.  1 pkt ⋅ Numer: pp-11921 ⋅ Poprawnie: 118/187 [63%] Rozwiąż 
Podpunkt 36.1 (1 pkt)
 Przyprostokątna AC trójkąta prostokątnego ABC ma długość 3, a przeciwprostokątna AB ma długość \sqrt{58}.

Wtedy tangens kąta ostrego CAB tego trójkąta jest równy:

Odpowiedzi:
A. \frac{\sqrt{58}}{7} B. \frac{3}{7}
C. \frac{7\sqrt{58}}{58} D. \frac{\sqrt{58}}{3}
E. \frac{3\sqrt{58}}{58} F. \frac{7}{3}
Zadanie 37.  1 pkt ⋅ Numer: pp-12042 ⋅ Poprawnie: 51/54 [94%] Rozwiąż 
Podpunkt 37.1 (1 pkt)
 Kąt \alpha jest ostry oraz \sin\alpha=\frac{21}{29}.

Wtedy \cos\alpha jest równy:

Odpowiedzi:
A. \frac{3}{58} B. \frac{1}{58}
C. \frac{23}{29} D. \frac{20}{29}
E. \frac{27}{29} F. \frac{9}{58}
Zadanie 38.  1 pkt ⋅ Numer: pp-12043 ⋅ Poprawnie: 48/54 [88%] Rozwiąż 
Podpunkt 38.1 (1 pkt)
 Dane są punkty M=(6,0), N=(6,7) O=(0,0).

Tangens kąta ostrego MON jest równy:

Odpowiedzi:
A. 1 B. \frac{7}{6}
C. \frac{1}{6} D. \frac{1}{2}
E. \frac{4}{3} F. \frac{3}{2}
Zadanie 39.  1 pkt ⋅ Numer: pp-12092 ⋅ Poprawnie: 9/17 [52%] Rozwiąż 
Podpunkt 39.1 (1 pkt)
 Kąt o mierze \alpha jest ostry i \tan\alpha=2\sqrt{3}.

Wtedy \cos\alpha jest równy:

Odpowiedzi:
A. \frac{\sqrt{13}}{13} B. \frac{\sqrt{13}}{26}
C. \frac{\sqrt{26}}{13} D. \frac{4\sqrt{13}}{39}
E. \frac{\sqrt{13}}{39} F. \frac{3\sqrt{13}}{26}
Zadanie 40.  1 pkt ⋅ Numer: pp-12122 ⋅ Poprawnie: 19/21 [90%] Rozwiąż 
Podpunkt 40.1 (1 pkt)
 Kąt \alpha jest ostry i \sin\alpha=\frac{3}{5}.

Wynika stąd, że \cos\alpha jest równy:

Odpowiedzi:
A. \frac{4}{25} B. \frac{4}{5}
C. \frac{\sqrt{2}}{400} D. \frac{\sqrt{2}}{10}
E. \frac{2}{5} F. \frac{16}{25}
Zadanie 41.  1 pkt ⋅ Numer: pp-12147 ⋅ Poprawnie: 105/123 [85%] Rozwiąż 
Podpunkt 41.1 (1 pkt)
 W trójkącie prostokątnym ABC sinus kąta CAB jest równy \frac{20}{29}, a przeciwprostokątna AB jest o 18 dłuższa od przyprostokątnej BC.

Długość przeciwprostokątnej AB tego trójkąta jest równa:

Odpowiedzi:
A. 62 B. 57
C. 55 D. 64
E. 58 F. 60
Zadanie 42.  2 pkt ⋅ Numer: pp-20269 ⋅ Poprawnie: 157/403 [38%] Rozwiąż 
Podpunkt 42.1 (2 pkt)
 » Kąt \alpha jest ostry oraz \cos\alpha=\frac{1}{2}.

Oblicz średnią arytmetyczną liczb a=\sin\alpha, b=\frac{1}{2} i c=\frac{1}{3}\tan\alpha.

Odpowiedź:
\overline{x}= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 43.  2 pkt ⋅ Numer: pp-20262 ⋅ Poprawnie: 328/521 [62%] Rozwiąż 
Podpunkt 43.1 (2 pkt)
 W pewnym trójkącie prostokątnym przyprostokątne mają długość 9 i 3, a jeden z kątów ostrych tego trójkąta ma miarę \alpha.

Oblicz \sin\alpha\cdot \cos\alpha.

Odpowiedź:
\sin\alpha\cdot\cos\alpha=
(wpisz dwie liczby całkowite)
Zadanie 44.  2 pkt ⋅ Numer: pp-20257 ⋅ Poprawnie: 71/150 [47%] Rozwiąż 
Podpunkt 44.1 (2 pkt)
 » Kąt \beta jest ostry oraz \tan\beta=\frac{48}{55}. Oblicz \sin\beta+\cos\beta.
Odpowiedź:
\sin\beta+\cos\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 45.  2 pkt ⋅ Numer: pp-20256 ⋅ Poprawnie: 32/112 [28%] Rozwiąż 
Podpunkt 45.1 (2 pkt)
 « Kąt \alpha jest ostry oraz \tan\alpha+16\cot\alpha=8.

Oblicz wartość wyrażenia \sin\alpha\cdot \cos\alpha.

Odpowiedź:
\sin\alpha\cdot\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 46.  2 pkt ⋅ Numer: pp-20255 ⋅ Poprawnie: 132/290 [45%] Rozwiąż 
Podpunkt 46.1 (2 pkt)
 « Kąt \beta jest ostry. Oblicz wartość wyrażenia 3+2\tan^2\beta.
Dane
\sin\beta=\frac{3}{4}=0.75000000000000
Odpowiedź:
3+2\tan^2\beta=
(wpisz dwie liczby całkowite)
Zadanie 47.  2 pkt ⋅ Numer: pp-20254 ⋅ Poprawnie: 107/202 [52%] Rozwiąż 
Podpunkt 47.1 (2 pkt)
 Kąt \beta jest ostry. Oblicz wartość wyrażenia \sin^2\beta-3\cos^2\beta.
Dane
\sin\beta=\frac{\sqrt{3}}{6}=0.28867513459481
Odpowiedź:
\sin^2\beta-3\cos^2\beta=
(wpisz dwie liczby całkowite)
Zadanie 48.  2 pkt ⋅ Numer: pp-20274 ⋅ Poprawnie: 197/450 [43%] Rozwiąż 
Podpunkt 48.1 (2 pkt)
 Kąt \alpha jest ostry. Oblicz wartość wyrażenia 2+\sin^3\alpha+\sin\alpha\cdot \cos^2\alpha.
Dane
\cos\alpha=\frac{\sqrt{5}}{5}=0.44721359549996
Odpowiedź:
Wpisz odpowiedź:  + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 49.  2 pkt ⋅ Numer: pp-20727 ⋅ Poprawnie: 57/176 [32%] Rozwiąż 
Podpunkt 49.1 (2 pkt)
 « Przekątne prostokąta maja długość d i przecinają się pod kątem o mierze \alpha.

Oblicz odległość wierzchołka prostokąta od przekątnej, do której wierzchołek ten nie należy (funkcję trygonometryczną kąta przyjmij z dokładnością do trzech miejsc po przecinku).

Dane
d=16
\alpha=43^{\circ}
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 50.  2 pkt ⋅ Numer: pp-20728 ⋅ Poprawnie: 52/129 [40%] Rozwiąż 
Podpunkt 50.1 (2 pkt)
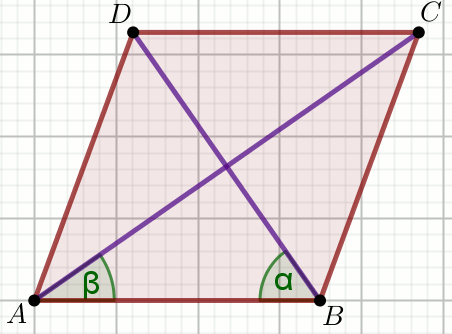
 W równoległoboku dany jest sinus kąta ostrego \alpha oraz wysokość h opuszczona na dłuższy bok tego równoległoboku. Stosunek długości sąsiednich boków tego równoległoboku wynosi k.

Oblicz długość obwodu tego równoległoboku.

Dane
\sin\alpha=\frac{6}{7}=0.85714285714286
h=20
k=\frac{9}{2}=4.50000000000000
Odpowiedź:
L=
(wpisz dwie liczby całkowite)
Zadanie 51.  2 pkt ⋅ Numer: pp-20729 ⋅ Poprawnie: 73/305 [23%] Rozwiąż 
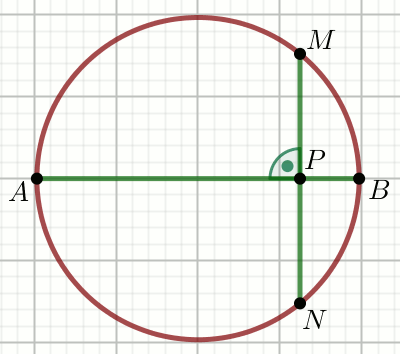
Podpunkt 51.1 (1 pkt)
 » Cięciwa AB jest średnicą okręgu na rysunku:

Oblicz \tan\sphericalangle ABM.

Dane
|AP|=16
|PB|=4
Odpowiedź:
\tan\sphericalangle ABM= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 51.2 (1 pkt)
 Oblicz \sin\sphericalangle MAB.
Odpowiedź:
\sin\sphericalangle MAB= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 52.  2 pkt ⋅ Numer: pp-20730 ⋅ Poprawnie: 107/257 [41%] Rozwiąż 
Podpunkt 52.1 (1 pkt)
 Czworokąt na rysunku jest rombem o obwodzie długości L:

Oblicz \cos\alpha.

Dane
L=360
|DB|=108
Odpowiedź:
\cos\alpha=
(wpisz dwie liczby całkowite)
Podpunkt 52.2 (1 pkt)
 Oblicz \tan\beta.
Odpowiedź:
\tan\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 53.  2 pkt ⋅ Numer: pp-20740 ⋅ Poprawnie: 46/392 [11%] Rozwiąż 
Podpunkt 53.1 (1 pkt)
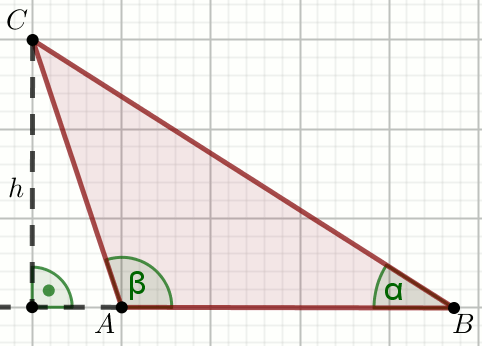
 « Dany jest trójkąt:

Oblicz |AC|. Do obliczeń użyj przybliżeń wartości funkcji trygonometrycznych z dokładnością do dwóch miejsc po przecinku.

Dane
\alpha=42^{\circ}
\beta=108^{\circ}
h=8
Odpowiedź:
|AC|=
(wpisz dwie liczby całkowite)
Podpunkt 53.2 (1 pkt)
 Oblicz |AB|. Do obliczeń użyj przybliżeń wartości funkcji trygonometrycznych z dokładnością do dwóch miejsc po przecinku.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 54.  2 pkt ⋅ Numer: pp-20278 ⋅ Poprawnie: 34/164 [20%] Rozwiąż 
Podpunkt 54.1 (2 pkt)
 W trójkącie prostokątnym ABC o przeciwprostokątnej AB kąt CAB ma miarę \alpha.

Oblicz pole koła opisanego na tym trójkącie.

Dane
\sin\alpha=\frac{13}{16}=0.81250000000000
|AC|=7
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 55.  2 pkt ⋅ Numer: pp-20288 ⋅ Poprawnie: 128/194 [65%] Rozwiąż 
Podpunkt 55.1 (2 pkt)
 W prostokątnym trójkącie ABC na przeciwprostokątnej AB wybrano punkt D, a na przyprostokątnej BC punkt E w taki sposób, że DE||AC oraz |BE|=|CE|=d.

Wyznacz tangens kąta EDC.

Dane
|AC|=20
d=10
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 56.  2 pkt ⋅ Numer: pp-20747 ⋅ Poprawnie: 35/101 [34%] Rozwiąż 
Podpunkt 56.1 (2 pkt)
 « W prostokątnym trójkącie ABC na przeciwprostokątnej AB wybrano punkt D, a na przyprostokątnej BC punkt E w taki sposób, że DE||AC.

Wyznacz tangens kąta ECD.

Dane
|AC|=20
|BE|=5
|CE|=8
Odpowiedź:
\tan\sphericalangle ECD=
(wpisz dwie liczby całkowite)
Zadanie 57.  2 pkt ⋅ Numer: pp-20283 ⋅ Poprawnie: 56/98 [57%] Rozwiąż 
Podpunkt 57.1 (1 pkt)
 Trójkąt ABC jest równoramienny o podstawie AB, a punkt D jest środkiem jego podstawy AB.

Oblicz miarę stopniową najmniejszego kąta tego trójkąta.

Dane
|CD|=\frac{\sqrt{7}}{2}=1.32287565553230
|AC|=\sqrt{7}=2.64575131106459
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Podpunkt 57.2 (1 pkt)
 Oblicz miarę stopniową największego kąta tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 58.  2 pkt ⋅ Numer: pp-20282 ⋅ Poprawnie: 84/172 [48%] Rozwiąż 
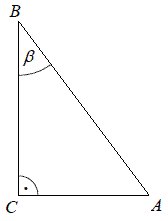
Podpunkt 58.1 (2 pkt)
 W trójkącie prostokątnym ABC kąt przy wierzchołku A jest prosty, a kąt przy wierzchołku B ma miarę \beta.

Oblicz \tan \beta.

Dane
\sin\beta=\frac{1}{5}=0.20000000000000
Odpowiedź:
\tan\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 59.  2 pkt ⋅ Numer: pp-20275 ⋅ Poprawnie: 65/133 [48%] Rozwiąż 
Podpunkt 59.1 (2 pkt)
 Kąty \alpha i \beta są kątami ostrymi w trójkącie prostokątnym.

Oblicz \tan\alpha\cdot \sin\beta.

Dane
\cos\alpha=\frac{3}{5}=0.60000000000000
Odpowiedź:
\tan\alpha\cdot\sin\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 60.  2 pkt ⋅ Numer: pp-20289 ⋅ Poprawnie: 198/416 [47%] Rozwiąż 
Podpunkt 60.1 (2 pkt)
 « Przyprostokątne trójkąta mają długości 4 i 5, a jeden z kątów ostrych tego trójkąta ma miarę \beta.

Oblicz \sin\beta\cdot \cos\beta.

Odpowiedź:
\sin\beta\cdot\cos\beta=
(wpisz dwie liczby całkowite)
Zadanie 61.  2 pkt ⋅ Numer: pp-21184 ⋅ Poprawnie: 133/183 [72%] Rozwiąż 
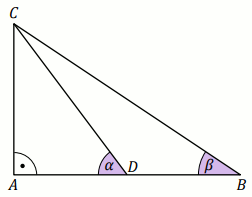
Podpunkt 61.1 (1 pkt)
 Dany jest trójkąt prostokątny ABC, w którym |AC|=8 i |BC|=10. Na przyprostokątnej AB leży taki punkt D, że |BD|=3 (zobacz rysunek).

Sinus kąta ostrego ABC jest równy:

Odpowiedzi:
A. \frac{16}{5} B. \frac{8}{5}
C. \frac{2}{5} D. \frac{4}{5}
E. \frac{1}{5} F. \frac{2\sqrt{2}}{5}
Podpunkt 61.2 (1 pkt)
 Tangens kąta ostrego ADC jest równy:
Odpowiedzi:
A. \frac{16}{3} B. \frac{4\sqrt{2}}{3}
C. \frac{8}{3} D. \frac{8}{9}
E. \frac{4}{3} F. \frac{2}{3}
Zadanie 62.  2 pkt ⋅ Numer: pp-21195 ⋅ Poprawnie: 190/410 [46%] Rozwiąż 
Podpunkt 62.1 (1 pkt)
 Dany jest trójkąt prostokątny ABC, w którym bok BC jest przeciwprostokątną, przyprostokątna AB ma długość 56, a środkowa CD ma długość 53. Oznaczmy kąt ADC przez \alpha, natomiast kąt ABC – przez \beta (zobacz rysunek).

Tangens kąta \alpha jest równy:

Odpowiedź:
\tan\alpha=
(wpisz dwie liczby całkowite)
Podpunkt 62.2 (1 pkt)
 Sinus kąta \beta jest równy:
Odpowiedź:
\sin\beta= \cdot√
(wpisz trzy liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm