⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Funkcje trygonometryczne kątów podstawowych
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- funkcje kątów podstawowych
- funkcje kątów w trojkątach podstawowych
- tabelka podstawowych wartości funkcji trygonometrycznych
| Zadanie 1. 1 pkt ⋅ Numer: pp-10639 ⋅ Poprawnie: 298/484 [61%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Oblicz wartość wyrażenia
\left(
\tan 30^{\circ}+\cot 60^{\circ}
\right)^2-\sin 30^{\circ}
.
Odpowiedź:
\left(\tan\alpha+\cot\beta\right)^2-\sin\gamma=
(liczba zapisana dziesiętnie)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10616 ⋅ Poprawnie: 365/597 [61%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Oblicz wartośc wyrażenia
w=
\tan^{2}30^{\circ}-\sin 60^{\circ}\cdot \cos 30^{\circ}-\sin 30^{\circ}\cdot \tan 30^{\circ}
.
Odpowiedź:
w=
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10674 ⋅ Poprawnie: 264/697 [37%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Przekątna równoległoboku o kącie ostrym \alpha o mierze
60^{\circ} i wysokości o długości
4\sqrt{3}, tworzy kąt prosty z jego bokiem.
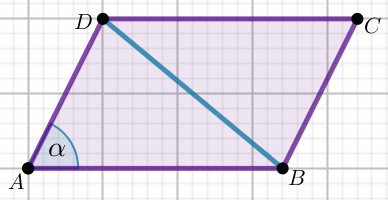
Oblicz obwód tego równoległoboku.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10662 ⋅ Poprawnie: 341/475 [71%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Zapisz obwód trójkąta ABC w postaci p\cdot a:
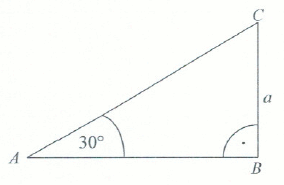
Podaj p.
Odpowiedź:
p=
+
\cdot
√
(wpisz trzy liczby całkowite)
(wpisz trzy liczby całkowite)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10660 ⋅ Poprawnie: 145/192 [75%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
» W trapezie prostokątnym ABCD długość
ramienia BC jest dwa razy większa od różnicy
długości jego podstaw.
Wyznacz miarę stopniową kąta ABC.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 1 pkt ⋅ Numer: pp-10657 ⋅ Poprawnie: 566/663 [85%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Przyprostokątne w trójkącie prostokątnym mają długości
1 oraz
\sqrt{3}.
Wyznacz miarę stopniową najmniejszego kąta w tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 1 pkt ⋅ Numer: pp-12393 ⋅ Poprawnie: 15/39 [38%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Dany jest trójkąt ABC, w którym |AB|=7,
|BC|=8 oraz |\sphericalangle ABC|=60^{\circ} (zobacz rysunek).
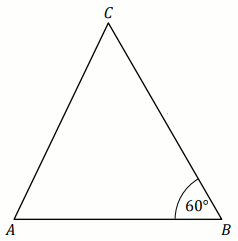
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : pole powierzchni trójkąta ABC jest równe 14\sqrt{3} | T/N : trójkąta ABC jest równoboczny |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20259 ⋅ Poprawnie: 165/275 [60%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Oblicz x-y, gdy
x=\sin^4{30^{\circ}}-\cos^4{30^{\circ}},
y=1-4\sin^2{30^{\circ}}\cdot \cos^2{30^{\circ}}.
Odpowiedź:
x-y=
(liczba zapisana dziesiętnie)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20731 ⋅ Poprawnie: 132/387 [34%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Czworokąt ABCD na rysunku jest trapezem,
a czworokąt EFCD prostokątem. Wiadomo, że
\alpha=120^{\circ}, \beta=150^{\circ} i
h=4.
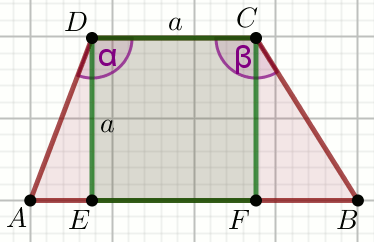
Oblicz obwód czworokąta ABCD.
Odpowiedź:
L_{ABCD}=
(liczba zapisana dziesiętnie)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20732 ⋅ Poprawnie: 176/451 [39%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
» Dany jest czworokąt, w którym \alpha=30^{\circ},
\beta=60^{\circ} i |DB|=3:
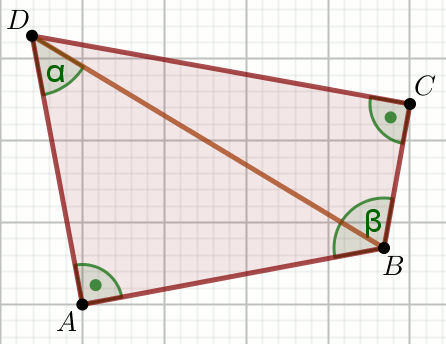
Oblicz długość obwodu czworokąta ABCD.
Odpowiedź:
L_{ABCD}=
(liczba zapisana dziesiętnie)
| Zadanie 11. 2 pkt ⋅ Numer: pp-20733 ⋅ Poprawnie: 109/391 [27%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Wyznacz wysokości trójkata ABC, w którym a=8
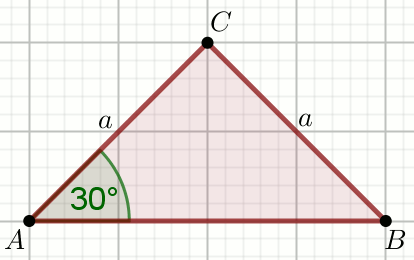
Podaj długość najkrótszej z wysokości tego trójkąta.
Odpowiedź:
| h_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 11.2 (1 pkt)
Podaj długość najdłuższej z wysokości tego trójkąta.
Odpowiedź:
| h_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 12. 2 pkt ⋅ Numer: pp-20741 ⋅ Poprawnie: 91/247 [36%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
Oblicz wartość wyrażenia
w=
(\tan{30^{\circ}}-\sin{60^{\circ}})(\cot{30^{\circ}}-\cos{45^{\circ}})
.
Odpowiedź:
| w= |
|
|
| (wpisz cztery liczby całkowite) | ||