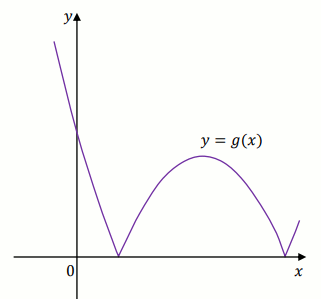Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Wykres, równania i nierówności kwadratowe z wartością bezwzględną

Zadania dla liceum ogólnokształcącego - poziom rozszerzony

 

Zadanie 1.  2 pkt ⋅ Numer: pr-20099 ⋅ Poprawnie: 15/25 [60%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 Rozwiąż równanie |x^2-16|+|x^2-36|=4x+a.

Podaj najmniejsze rozwiązanie tego równania.

Dane
a=-3
Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 1.2 (1 pkt)
 Podaj największe rozwiązanie tego równania.
Odpowiedź:
x_{max}= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 2.  2 pkt ⋅ Numer: pr-20100 ⋅ Poprawnie: 50/79 [63%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 » Rozwiąż równanie x^2+2ax+2x+|x+1+a|=11-2a-a^2 .

Podaj największe z rozwiązań tego równania.

Dane
a=-2
Odpowiedź:
x_{max}= (wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
 Podaj średnią arytmetyczną wszystkich rozwiązań tego równania.
Odpowiedź:
x_s= (wpisz liczbę całkowitą)
Zadanie 3.  2 pkt ⋅ Numer: pr-20101 ⋅ Poprawnie: 25/32 [78%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 « Rozwiąż równanie x^2+4x+2ax+a^2+4a+7=4|x+4+a| .

Podaj najmniejsze z rozwiązań tego równania.

Dane
a=-2
Odpowiedź:
x_{min}= (wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
 Podaj średnią arytmetyczną wszystkich rozwiązań tego równania.
Odpowiedź:
x_s= (wpisz liczbę całkowitą)
Zadanie 4.  2 pkt ⋅ Numer: pr-20102 ⋅ Poprawnie: 30/76 [39%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 Rozwiąż nierówność |x^2+3x+2|-|x-a|\leqslant 3.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejsze z rozwiązań tej nierówności.

Dane
a=3
Odpowiedź:
x_{min}= + \cdot √
(wpisz trzy liczby całkowite)
Podpunkt 4.2 (1 pkt)
 Podaj największą liczbę spełniającą tę nierówność.
Odpowiedź:
x_{max}= + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 5.  2 pkt ⋅ Numer: pr-20103 ⋅ Poprawnie: 52/118 [44%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 « Rozwiąż nierówność (x+6-a)^2-3|x-a| > 0 .

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.

Dane
a=-4
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Podpunkt 5.2 (1 pkt)
 Podaj największą liczbę, która nie spełnia tej nierówności.
Odpowiedź:
max= (wpisz liczbę całkowitą)
Zadanie 6.  2 pkt ⋅ Numer: pr-20104 ⋅ Poprawnie: 20/44 [45%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 « Wyznacz zbiór liczb, które nie spełniają nierówności (x+1-a)^2-|x-a|\geqslant 2x-2a+1 .

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.

Dane
a=-4
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
 Jaka jest łączna długość tych przedziałów.
Odpowiedź:
d= (wpisz liczbę całkowitą)
Zadanie 7.  4 pkt ⋅ Numer: pr-30074 ⋅ Poprawnie: 7/18 [38%] Rozwiąż 
Podpunkt 7.1 (2 pkt)
 » Rozwiąż nierówność \sqrt{(2+a-x)^2(6+a-x)^2}-3x+6+3a > 0 .

Podaj największą liczbę, która nie spełnia tej nierówności.

Dane
a=-3
Odpowiedź:
max= (wpisz liczbę całkowitą)
Podpunkt 7.2 (2 pkt)
 Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Zadanie 8.  4 pkt ⋅ Numer: pr-30075 ⋅ Poprawnie: 30/39 [76%] Rozwiąż 
Podpunkt 8.1 (2 pkt)
 « Rozwiąż równanie x^2-(a+6)x+\left|x-3-\frac{a}{2}\right|+\frac{1}{4}a^2+3a-3=0 .

Podaj najmniejsze rozwiązanie tego równania.

Dane
a=-5
Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
 Podaj największe rozwiązanie tego równania.
Odpowiedź:
x_{max}=
(wpisz dwie liczby całkowite)
Zadanie 9.  4 pkt ⋅ Numer: pr-30076 ⋅ Poprawnie: 15/20 [75%] Rozwiąż 
Podpunkt 9.1 (2 pkt)
 Rozwiąż równanie x^2+(4-2a)x-4|x+4-a|+a^2-4a+7=0 .

Podaj sumę wszystkich rozwiązań tego równania.

Dane
a=-2
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Podpunkt 9.2 (2 pkt)
 Podaj sumę kwadratów wszystkich rozwiązań tego równania.
Odpowiedź:
s= (wpisz liczbę całkowitą)
Zadanie 10.  4 pkt ⋅ Numer: pr-30077 ⋅ Poprawnie: 8/20 [40%] Rozwiąż 
Podpunkt 10.1 (2 pkt)
 « Rozwiąż nierówność x^2+2ax-3|x+6+a|+a^2 > 0 .

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.

Dane
a=-2
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Podpunkt 10.2 (2 pkt)
 Przedział \langle p, q\rangle jest zbiorem tych wszystkich wartości x, które nie spełniają podanej nierówności.

Podaj środek tego przedziału.

Odpowiedź:
x_s=
(wpisz dwie liczby całkowite)
Zadanie 11.  4 pkt ⋅ Numer: pr-30078 ⋅ Poprawnie: 30/39 [76%] Rozwiąż 
Podpunkt 11.1 (2 pkt)
 Rozwiąż nierówność ax^2+b|x|+c \lessdot 0 .

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów, które są liczbami ujemnymi.

Dane
a=1
b=-10.5
c=26.0
Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 11.2 (2 pkt)
 Podaj sumę wszystkich końców liczbowych tych przedziałów, które są liczbami dodatnimi.
Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 12.  4 pkt ⋅ Numer: pr-30079 ⋅ Poprawnie: 13/19 [68%] Rozwiąż 
Podpunkt 12.1 (2 pkt)
 « Rozwiąż nierówność x^2-2ax+a^2+c \leqslant -b|x-a| .

Podaj najmniejsze rozwiązanie tej nierówności.

Dane
b=-1
c=-12
a=3
Odpowiedź:
x_{min}= (wpisz liczbę całkowitą)
Podpunkt 12.2 (2 pkt)
 Podaj największe rozwiązanie tej nierówności.
Odpowiedź:
x_{max}= (wpisz liczbę całkowitą)
Zadanie 13.  4 pkt ⋅ Numer: pr-30080 ⋅ Poprawnie: 7/13 [53%] Rozwiąż 
Podpunkt 13.1 (2 pkt)
 » Rozwiąż nierówność x^2+(6+2a)x+|x+2+a|+a^2+6a+8\leqslant 0 .

Podaj najmniejsze rozwiązanie tej nierówności.

Dane
a=-8
Odpowiedź:
x_{min}= (wpisz liczbę całkowitą)
Podpunkt 13.2 (2 pkt)
 Podaj największe rozwiązanie tej nierówności.
Odpowiedź:
x_{max}= (wpisz liczbę całkowitą)
Zadanie 14.  4 pkt ⋅ Numer: pr-30081 ⋅ Poprawnie: 61/161 [37%] Rozwiąż 
Podpunkt 14.1 (2 pkt)
 « Rozwiąż nierówność |x^2-2ax| \lessdot b .

Rozwiązanie zapisz w postaci sumy predziałów. Podaj sumę wszystkich końców tych przedziałów, które są liczbami całkowitymi.

Dane
a=5
b=25
Odpowiedź:
suma= (wpisz liczbę całkowitą)
Podpunkt 14.2 (2 pkt)
 Podaj najmniejszy z końców liczbowych tych przedziałów, który nie jest liczbą całkowitą.
Odpowiedź:
min= + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 15.  4 pkt ⋅ Numer: pr-30082 ⋅ Poprawnie: 17/29 [58%] Rozwiąż 
Podpunkt 15.1 (2 pkt)
 Rozwiąż nierówność \left|x^2+(a+6)x+\frac{a^2}{4}+3a-1\right| \leqslant 6 .

Rozwiązaniem tej nierówności jest zbiór \langle x_1, x_2\rangle\cup\langle x_3, x_4\rangle\, gdzie x_2\lessdot x_3. Podaj x_1+x_2.

Dane
a=3
Odpowiedź:
x_1+x_2= (wpisz liczbę całkowitą)
Podpunkt 15.2 (2 pkt)
 Podaj x_3.
Odpowiedź:
x_{3}=
(wpisz dwie liczby całkowite)
Zadanie 16.  4 pkt ⋅ Numer: pr-31016 ⋅ Poprawnie: 1/1 [100%] Rozwiąż 
Podpunkt 16.1 (2 pkt)
 Funkcja g jest określona wzorem g(x)=\left|-\frac{1}{4}x^2+3x-5\right| dla każdego x\in\mathbb{R}. Fragment wykresu funkcji g w kartezjańskim układzie współrzędnych (x,y) przedstawiono na rysunku (jednostki pominięto).

Wyznacz zbiór wszystkich wartości, jakie funkcja g przyjmuje w przedziale \left[9,11\right].

Rozwiązanie zapisz w postaci przedziału [a,b]. Podaj końce tego przedziału.

Odpowiedzi:
a= (dwie liczby całkowite)
b= (dwie liczby całkowite)
Podpunkt 16.2 (2 pkt)
 Wyznacz zbiór wszystkich wartości parametru m, dla których równanie g(x)=|m| ma dokładnie dwa rozwiązania, oba dodatnie.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy ujemny i najmniejszy dodatni koniec tych przedziałów.

Odpowiedzi:
min_{\lessdot 0}= (dwie liczby całkowite)
min_{> 0}= (dwie liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm