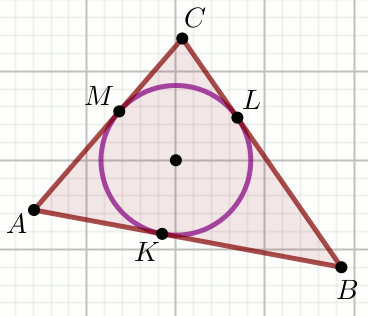
Okrąg wpisany w trójkąt
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
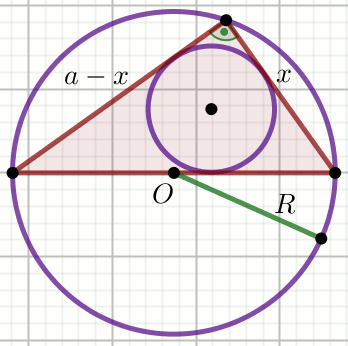
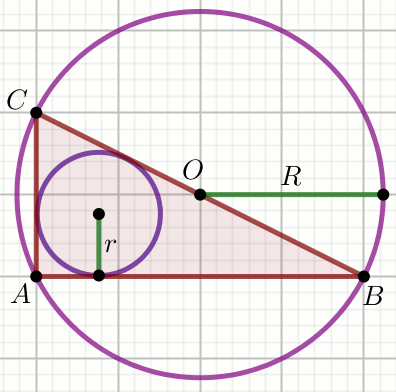
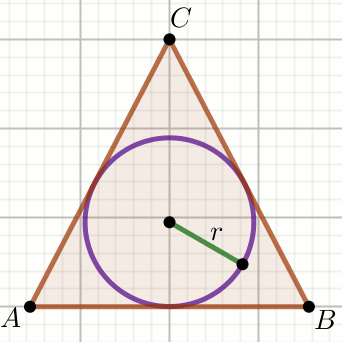
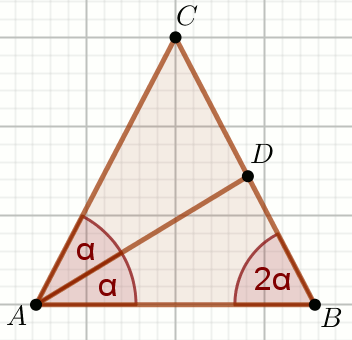
okrąg wpisany
dwusieczne kątów trójkąta
środek okręgu wpisanego w trójkąt
promień okręgu wpisanego w trójkąt
twierdzenie o dwusiecznej trójkąta
Zadanie 1. 2 pkt ⋅ Numer: pp-20717 ⋅ Poprawnie: 47/188 [25%]
Rozwiąż
Podpunkt 1.1 (2 pkt)
« Długość promienia okręgu opisanego na trójkącie równobocznym jest o
d większa od długości promienia okręgu
wpisanego w ten trójkąt.
Oblicz pole powierzchni tego trójkąta.
Dane
d=8\sqrt{6}=19.59591794226542
Odpowiedź:
P_{\triangle}=
\cdot √
(wpisz dwie liczby całkowite)
Zadanie 2. 2 pkt ⋅ Numer: pp-20218 ⋅ Poprawnie: 23/58 [39%]
Rozwiąż
Podpunkt 2.1 (2 pkt)
Sprawdź, czy koło o polu powierzchni
P
mieści się w trójkącie o bokach długości
a ,
b i
c .
Jeśli tak, to podaj promień tego koła, jeśli nie, to wpisz liczbę, o którą
należało by skrócić promień tego koła, aby zmieściło się w tym trójkącie.
Dane
a=9 b=15 c=\sqrt{306}=17.49285568453590 P=\sqrt{3}\cdot \pi=5.441398092703
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 3. 2 pkt ⋅ Numer: pp-20719 ⋅ Poprawnie: 125/276 [45%]
Rozwiąż
Podpunkt 3.1 (2 pkt)
Punkt
O jest środkiem okręgu opisanego na trójkącie:
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Dane
a=97 R=\frac{85}{2}=42.50
Odpowiedź:
r=
(wpisz liczbę całkowitą)
Zadanie 4. 2 pkt ⋅ Numer: pp-20721 ⋅ Poprawnie: 194/325 [59%]
Rozwiąż
Podpunkt 4.1 (2 pkt)
Punkt
O jest środkiem okręgu:
Oblicz r+R .
Dane
|AC|=84 |AB|=13
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 5. 2 pkt ⋅ Numer: pp-20963 ⋅ Poprawnie: 23/55 [41%]
Rozwiąż
Podpunkt 5.1 (1 pkt)
W trójkąt prostokątny o przyprostokątnych długości
16 i
30 wpisano okrąg.
Oblicz długości odcinków, na które punkt styczności podzielił przeciwprostokątną tego trójkąta.
Odpowiedzi:
Podpunkt 5.2 (0.5 pkt)
Dwusieczna kąta prostego przecina przeciwprostokątną tego trójkąta w punkcie
P .
Oblicz długości odcinków, na które dzieli przeciwprostokątną punkt P .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 5.3 (0.5 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 6. 2 pkt ⋅ Numer: pp-21011 ⋅ Poprawnie: 2/4 [50%]
Rozwiąż
Podpunkt 6.1 (0.5 pkt)
W trójkąt prostokątny o przyprostokątnych długości
13 i
84 wpisano okrąg.
Wyznacz długości odcinków, na jakie dwusieczna kąta prostego podzieliła przeciwprostokątną tego trójkąta.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 6.2 (0.5 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 6.3 (1 pkt)
Wyznacz długości odcinków, na jakie punkt styczności okręgu z przeciwprostokątną podzielił tę przeciwprostokątną.
Odpowiedzi:
Zadanie 7. 2 pkt ⋅ Numer: pp-21012 ⋅ Poprawnie: 17/48 [35%]
Rozwiąż
Podpunkt 7.1 (1 pkt)
W trójkącie prostokątnym dwusieczna kąta prostego podzieliła przeciwprostokątną tego trójkata
na odcinki o długości
\frac{369}{49} i
\frac{1640}{49} .
Wyznacz długości przyprostokątnych tego trójkąta.
Odpowiedzi:
Podpunkt 7.2 (1 pkt)
Oblicz długość odcinka tej dwusiecznej zawartego w tym trójkącie.
Odpowiedź:
Zadanie 8. 3 pkt ⋅ Numer: pp-21017 ⋅ Poprawnie: 17/51 [33%]
Rozwiąż
Podpunkt 8.1 (1 pkt)
W trójkącie prostokątnym najkrótsza wysokość ma długość
660 ,
a najkrótszy bok ma długość
671 .
Oblicz długości dwóch pozostałych boków tego trójkąta.
Odpowiedzi:
Podpunkt 8.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 8.3 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten okrąg.
Odpowiedź:
r=
(wpisz liczbę całkowitą)
Zadanie 9. 2 pkt ⋅ Numer: pp-21018 ⋅ Poprawnie: 5/8 [62%]
Rozwiąż
Podpunkt 9.1 (1 pkt)
W trójkącie prostokątnym spodek najkrótszej wysokości dzieli przeciwprostokątną tego trójkąta
na dwa odcinki, których długości pozostają w stosunku
1:49 . Wiedząc, że promień okręgu opisanego na tym
trójkącie ma długość
5\sqrt{2} oblicz długości
przyprostokątnych tego trójkąta.
Podaj wyznaczone długości przyprostokątnych.
Odpowiedzi:
Podpunkt 9.2 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
Zadanie 10. 2 pkt ⋅ Numer: pp-21021 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 10.1 (2 pkt)
Obwód trójkąta prostokątnego ma długość
182 . Na trójkącie tym opisano okrąg
o promieniu
R i w trójkąt ten wpisano okrąg o promieniu długości
r .
Podaj długości tych promieni.
Odpowiedzi:
Zadanie 11. 2 pkt ⋅ Numer: pp-21203 ⋅ Poprawnie: 214/248 [86%]
Rozwiąż
Podpunkt 11.1 (1 pkt)
Dany jest trójkąt prostokątny o bokach długości
13 ,
84 oraz
85 .
Długość promienia okręgu wpisanego w ten trójkąt jest równa:
Odpowiedzi:
A. 8
B. \frac{13}{2}
C. \frac{11}{2}
D. 9
E. \frac{9}{2}
F. 6
G. \frac{15}{2}
H. 5
Podpunkt 11.2 (1 pkt)
Długość promienia okręgu opisanego na tym trójkącie jest równa:
Odpowiedzi:
A. 43
B. \frac{85}{2}
C. 42
D. \frac{91}{2}
E. \frac{83}{2}
F. 41
G. 44
H. \frac{89}{2}
Zadanie 12. 2 pkt ⋅ Numer: pp-20217 ⋅ Poprawnie: 19/68 [27%]
Rozwiąż
Podpunkt 12.1 (2 pkt)
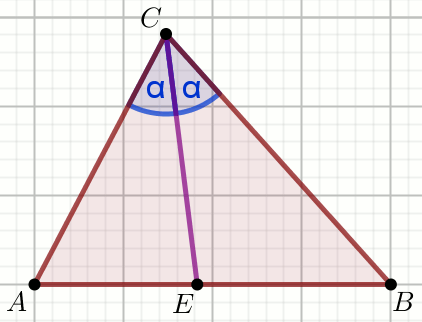
«« Trójkąt równoramienny
ABC o podstawie
AB jest ostrokątny. W trójkąt ten wpisano okrąg
o środku
S , przy czym kąt
|\sphericalangle SAB|=\alpha .
Oblicz |\sphericalangle BCA| .
Dane
\alpha=35^{\circ}
Odpowiedź:
|\sphericalangle BCA|=
(wpisz liczbę całkowitą)
Zadanie 13. 2 pkt ⋅ Numer: pp-20720 ⋅ Poprawnie: 245/594 [41%]
Rozwiąż
Podpunkt 13.1 (2 pkt)
« Dany jest trójkąt:
Oblicz r .
Dane
|AB|=168 |AC|=85 |BC|=85
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 14. 3 pkt ⋅ Numer: pp-20960 ⋅ Poprawnie: 14/60 [23%]
Rozwiąż
Podpunkt 14.1 (1 pkt)
Dany jest trójkąt ostrokątny
ABC , w którym
|CD|=\frac{625}{39} i
|BD|=\frac{350}{39} :
Oblicz |AB| .
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 14.3 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 15. 2 pkt ⋅ Numer: pp-20962 ⋅ Poprawnie: 7/14 [50%]
Rozwiąż
Podpunkt 15.1 (1 pkt)
W trójkącie równoramiennym
ABC , w którym
|AC|=|BC| ,
dwusieczna kąta o wierzchołku
A przeciecięła bok
BC
w punkcie
D takim, że
|BD|=\frac{10}{3} i
|CD|=\frac{50}{3} .
Oblicz długość podstawy AB tego trójkąta.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
Odcinek
DE jest wysokością trójkąta
ABD .
Oblicz długość odcinka EB .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 16. 2 pkt ⋅ Numer: pp-21013 ⋅ Poprawnie: 3/8 [37%]
Rozwiąż
Podpunkt 16.1 (1 pkt)
« W trójkącie równoramiennym
ABC o podstawie
AB
dane są długości boków:
|AC|=|BC|=34 i
|AB|=32 .
W trójkąt ten wpisano okrąg.
Oblicz długości odcinków, na które dwusieczna kąta przy podstawie podzieliła ramię tego trójkąta.
Odpowiedzi:
Podpunkt 16.2 (1 pkt)
Oblicz długości odcinków, na które punkt styczności okręgu z ramieniem trójkąta podzielił to ramię.
Odpowiedzi:
Zadanie 17. 2 pkt ⋅ Numer: pp-21022 ⋅ Poprawnie: 2/5 [40%]
Rozwiąż
Podpunkt 17.1 (1 pkt)
W trójkącie równoramiennym
ABC , w którym
|AC|=|BC| ,
wysokość
CD ma długośc
84 , a promień okręgu
wpisanego w ten trójkąt ma długość
\frac{78}{7} .
Oblicz długość boku AB .
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
Zadanie 18. 2 pkt ⋅ Numer: pp-20718 ⋅ Poprawnie: 184/409 [44%]
Rozwiąż
Podpunkt 18.1 (1 pkt)
Dany jest trójkąt:
Oblicz |AK| :
Dane
|AB|=18 |BC|=34 |AC|=32
Odpowiedź:
|AK|=
(wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
Odpowiedź:
|BL|=
(wpisz liczbę całkowitą)
Zadanie 19. 2 pkt ⋅ Numer: pp-20237 ⋅ Poprawnie: 3/15 [20%]
Rozwiąż
Podpunkt 19.1 (2 pkt)
Środkowa
CD trójkata
ABC
jest prostopadła do dwusiecznej
AE tego trójkata.
Oblicz stosunek \frac{|AC|}{|AB|} .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 20. 2 pkt ⋅ Numer: pp-20961 ⋅ Poprawnie: 6/8 [75%]
Rozwiąż
Podpunkt 20.1 (2 pkt)
Różnica długości dwóch boków trójkąta jest równa
12 .
Dwusieczna kąta utworzonego przez te boki przecina trzeci bok trójkąta w punkcie, który
dzieli ten bok w stosunku
\frac{13}{10} .
Oblicz długości tych dwóch boków.
Odpowiedzi:
Zadanie 21. 2 pkt ⋅ Numer: pp-21010 ⋅ Poprawnie: 16/31 [51%]
Rozwiąż
Podpunkt 21.1 (2 pkt)
«« Dany jest trójkąt:
Oblicz |AE| .
Dane
|AB|=\frac{12}{5}=2.40000000000000 |AC|=\frac{6}{5}=1.20000000000000 |BC|=2=2.00000000000000
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 22. 4 pkt ⋅ Numer: pp-30015 ⋅ Poprawnie: 39/137 [28%]
Rozwiąż
Podpunkt 22.1 (4 pkt)
«« Trójkąt
ABC jest prostokątny i jedna z jego
przyprostokątnych jest dwa razy dłuższa od drugiej, a środkowa
CD ma długość
d .
Wiedząc, że |\sphericalangle C|=90^{\circ} oblicz
promień okręgu wpisanego w ten trójkąt.
Dane
d=5\sqrt{5}=11.180339887498948
Odpowiedź:
Zadanie 23. 4 pkt ⋅ Numer: pp-30024 ⋅ Poprawnie: 41/96 [42%]
Rozwiąż
Podpunkt 23.1 (4 pkt)
» Ze skrawka materiału w kształcie trójkąta o długościach boków
a cm,
b cm i
c cm wycięto koło wpisane w ten trójkąt.
Ile cm2 materiału pozostało?
Dane
a=28 b=96 c=100
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 24. 4 pkt ⋅ Numer: pp-30298 ⋅ Poprawnie: 15/79 [18%]
Rozwiąż
Podpunkt 24.1 (4 pkt)
« Trójkąt
ABC jest prostokątny i jedna z jego
przyprostokątnych jest dwa razy dłuższa od drugiej, a wysokość
CD ma długość
d .
Wiedząc, że |\sphericalangle C|=90^{\circ} oblicz
promień okręgu wpisanego w ten trójkąt.
Dane
d=5\sqrt{5}=11.180339887498948
Odpowiedź:
Zadanie 25. 4 pkt ⋅ Numer: pp-30401 ⋅ Poprawnie: 8/34 [23%]
Rozwiąż
Podpunkt 25.1 (1 pkt)
W trójkącie równoramiennym
ABC podstawa
AB
ma długość
24 , a wysokość
AD długość
19.2 . Dwusieczna kąta
ABC przecina bok
AC w punkcie
P .
Oblicz długość ramion tego trójkąta.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
Podpunkt 25.2 (1 pkt)
Oblicz długość odcinków
AP i
CP .
Odpowiedzi:
Podpunkt 25.3 (2 pkt)
Oblicz długość odcinka
BP .
Odpowiedź:
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm