⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Twierdzenie sinusów
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- twierdzenie sinusów
- wzór sinusów
- funkcje trygonometryczne w dowolnym trójkącie
- promień okręgu opisanego na trójkącie
- rozwiązywanie trójkątów
- związki miarowe w trójkącie
| Zadanie 1. 2 pkt ⋅ Numer: pp-20890 ⋅ Poprawnie: 211/342 [61%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
« Dany jest trójkąt, w którym:
\sin\alpha=\frac{1}{2},
\cos\beta=\frac{1}{3} i
|BC|=12:
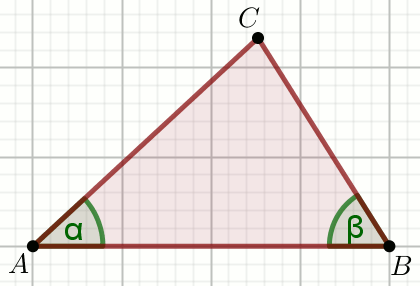
Oblicz |AC|.
Odpowiedź:
| |AC|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 2 pkt ⋅ Numer: pp-20891 ⋅ Poprawnie: 90/153 [58%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
« W trójkącie ABC, w którym
|AB|=96, |AC|=52 i
\cos\alpha=\frac{12}{13}, promień okręgu opisanego
na tym trójkącie ma długość \frac{338}{5}:
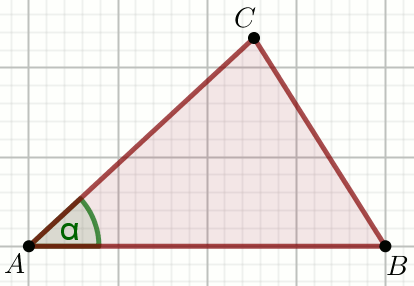
Oblicz sumę sinusów wszystkich kątów tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pp-20892 ⋅ Poprawnie: 98/220 [44%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
« Dany jest trójkąt, w którym |AB|=\frac{12\sqrt{10}}{5},
|BC|=\frac{12\sqrt{5}}{5},
|AC|=\frac{6\sqrt{10}}{5}+\frac{6\sqrt{30}}{5} i
\alpha=30^{\circ}:
Oblicz miarę stopniową największego kąta tego trójkąta.
Odpowiedź:
\beta_{max}\ [^{\circ}]=
(wpisz liczbę całkowitą)