⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Czworokąty - trapezoidy
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- czworokąty
- trapezoidy
- obwód czworokąta
- planimetria
| Zadanie 1. 2 pkt ⋅ Numer: pr-20108 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (2 pkt)
» Suma długości przekątnych czworokąta wynosi 156.
Jedna z przekątnych dzieli ten czworokąt na dwa trójkąty, których obwody
są równe 120 i 240.
Druga z przekątnych tego czworokąta dzieli go na dwa trójkąty, których obwody
są równe 180 i 300.
Oblicz długość obwodu tego czworokąta.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20109 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Obwód czworokąta ABCD jest równy
123. Trójkąt ABC jest
równoramienny o podstawie AC, zaś trójkąt
ACD jest równoramienny o podstawie
CD. Znane są również obwody obu tych trójkątów:
L_{ABC}=104 oraz L_{ACD}=83.
Podaj długość najkrótszego boku czworokąta ABCD.
Odpowiedź:
a_{min}=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
Podaj długość najdłuższego boku czworokąta ABCD.
Odpowiedź:
a_{max}=
(wpisz liczbę całkowitą)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20110 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Punkt przecięcia przekątnych deltoidu o długościach
160 i 210 dzieli przekątną
zawartą w osi symetrii tego deltoidu w stosunku
5:2.
Podaj długość obwodu tego deltoidu.
Odpowiedź:
| L= | |
| Zadanie 4. 2 pkt ⋅ Numer: pr-20764 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Zielone odcinki na rysunku są dwusiecznymi kątów wewnętrznych
czworokąta wypukłego, przy czym \gamma\neq 180^{\circ}:
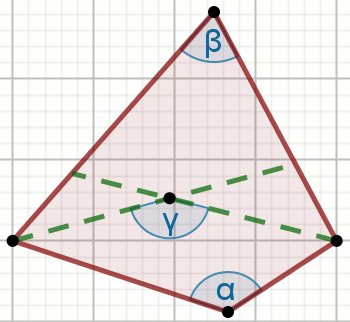
Wyraź miarę kąta \alpha w postaci \alpha=360^{\circ}+a\beta+b\gamma.
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)