Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Czworokąty - trapezy

Zadania dla liceum ogólnokształcącego - poziom rozszerzony

 

Zadanie 1.  2 pkt ⋅ Numer: pr-20111 ⋅ Poprawnie: 4/12 [33%] Rozwiąż 
Podpunkt 1.1 (2 pkt)
 » Przedstawiony na rysunku czworokąt jest trapezem równoramiennym, w którym |AB|=32, |CD|=8, |DO|=8 i |OB|=32:

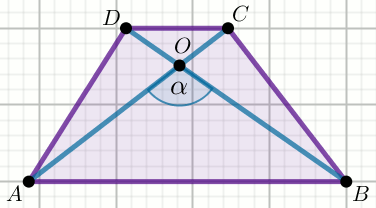
Oblicz \cos \alpha.

Odpowiedź:
\cos\alpha=
(wpisz dwie liczby całkowite)
Zadanie 2.  2 pkt ⋅ Numer: pr-20112 ⋅ Poprawnie: 4/12 [33%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Przedstawiony na rysunku czworokąt jest trapezem, w którym |AD|=|CD|=|BC|=11\sqrt{2}:

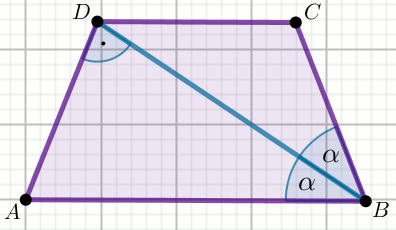
Oblicz sinus kąta ostrego tego trapezu.

Odpowiedź:
\sin2\alpha= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 2.2 (1 pkt)
 Oblicz długość wysokości tego trapezu.
Odpowiedź:
h= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 3.  2 pkt ⋅ Numer: pr-20113 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 3.1 (2 pkt)
 « Czworokąt na rysunku jest trapezem równoramiennym, w którym |BD|=\sqrt{91} i |DE|=3\sqrt{3}:

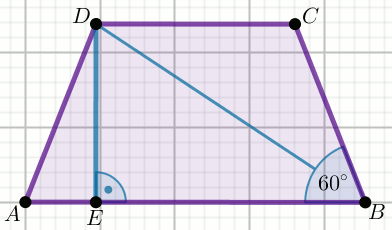
Wyznacz długość obwodu tego trapezu.

Odpowiedź:
L= (wpisz liczbę całkowitą)
Zadanie 4.  2 pkt ⋅ Numer: pr-20114 ⋅ Poprawnie: 4/12 [33%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 » Czworokąt na rysunku jest trapezem równoramiennym, a punkty A i B środkami jego ramion. Wiadomo, że a=6, b=24, c=18 i d=60:

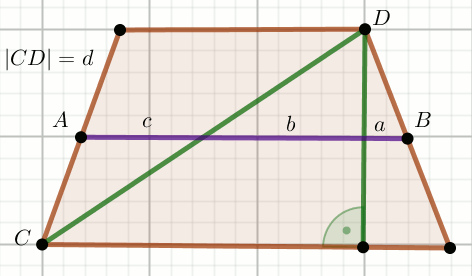
Wyznacz długość ramienia tego trapezu.

Odpowiedź:
Wpisz odpowiedź:  \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 4.2 (1 pkt)
 Oblicz obwód tego trapezu.
Odpowiedź:
L= + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 5.  4 pkt ⋅ Numer: pr-30091 ⋅ Poprawnie: 4/12 [33%] Rozwiąż 
Podpunkt 5.1 (4 pkt)
 « Czworokąt na rysunku jest trapezem, w którym a=\frac{15}{2}:

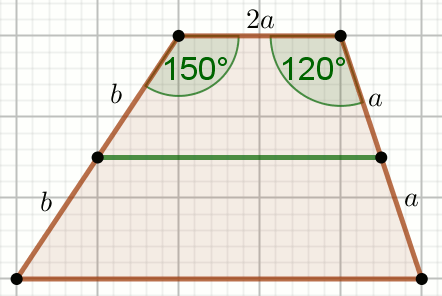
Oblicz długość zielonego odcinka.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 6.  4 pkt ⋅ Numer: pr-30092 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 6.1 (4 pkt)
 Czworokąt na rysunku jest trapezem równoramiennym, w którym |AB|=1 i |DC|=\frac{3}{4}, a punkty K i L są środkami zaznaczonych odcinków:

Oblicz |KL|.

Odpowiedź:
|KL|=
(wpisz dwie liczby całkowite)
Zadanie 7.  4 pkt ⋅ Numer: pr-30093 ⋅ Poprawnie: 4/11 [36%] Rozwiąż 
Podpunkt 7.1 (2 pkt)
 » Czworokąt na rysunku jest trapezem, w którym |CD|=9 i |AC|=9+9\sqrt{3}:

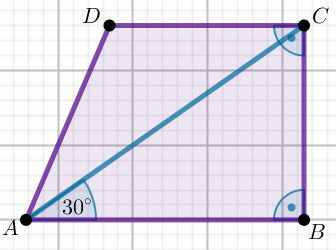
Wyznacz promień okręgu wpisanego w trójkąt ABC.

Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Podpunkt 7.2 (2 pkt)
 Oblicz sinus kąta rozwartego tego trapezu.
Odpowiedź:
\sin\sphericalangle ADC= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 8.  4 pkt ⋅ Numer: pr-30094 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 8.1 (2 pkt)
 Czworokąt na rysunku jest trapezem, w którym |CD|=20, |AD|=15 i |AC|=25:

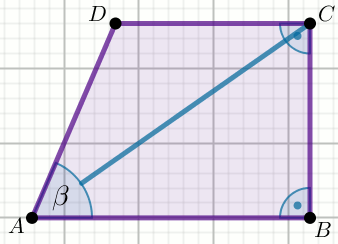
Oblicz \cos\beta.

Odpowiedź:
\cos\beta=
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
 Jaką długość ma odcinek łączący środki jego ramion?
Odpowiedź:
d=
(wpisz dwie liczby całkowite)
Zadanie 9.  4 pkt ⋅ Numer: pr-30825 ⋅ Poprawnie: 4/12 [33%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 (1 pkt) Czworokąt na rysunku jest trapezem, w którym |AD|=29 oraz \cos\alpha=\frac{20}{29}. W trapez ten wpisano okrąg:

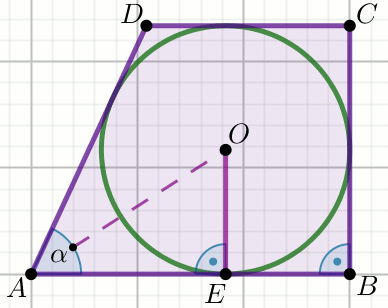
Wyznacz promień okręgu wpisanego w ten czworokąt.

Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Podpunkt 9.2 (1 pkt)
 (1 pkt) Oblicz pole powierzchni tego trapezu.
Odpowiedź:
P= (wpisz liczbę całkowitą)
Podpunkt 9.3 (2 pkt)
 (2 pkt) Wyznacz długość promienia okręgu opisanego na trójkącie AEO.
Odpowiedź:
R= \cdot√
(wpisz trzy liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm