Pole powierzchni kwadratu i prostokąta
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- pole powierzchni kwadratu
- pole powierzchni prostokąta
- wzory na pole
- własności pola powierzchni
| Zadanie 1. 1 pkt ⋅ Numer: pp-11095 ⋅ Poprawnie: 126/210 [60%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Pole prostokąta jest równe P, a jego przekątna
ma długość d. Wyznacz długość dłuższego boku tego prostokąta i zapisz
wynik w najprostszej postaci \frac{a\sqrt{b}}{c}, gdzie
a,b,c\in\mathbb{N}.
Podaj liczby a i c.
Dane
P=25\sqrt{3}=43.30127018922193
d=10
d=10
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11494 ⋅ Poprawnie: 241/293 [82%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Pole kwadratu ABCDjest równe
36. Kwadrat KLMN
jest obrazem kwadratu ABCD w podobieństwie o skali
k=\frac{1}{2}.
Oblicz długość przekątnej kwadratu KLMN.
Odpowiedź:
| |KM|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 1 pkt ⋅ Numer: pp-11491 ⋅ Poprawnie: 179/264 [67%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Przekątna kwadratu ma długość 3+2\sqrt{3}.
Oblicz pole powierzchni tego kwadratu.
Odpowiedź:
| P_{\square}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-11492 ⋅ Poprawnie: 74/92 [80%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Działka ma kształt prostokąta o powierzchni
6.00 ha i szerokości
200m.
Wymiary działki na planie wykonanym w skali 1 : 1000 są równe
mcm x ncm.
Podaj liczby m i n.
Odpowiedzi:
| min(m,n) | = |
(wpisz liczbę całkowitą) |
| max(m,n) | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11099 ⋅ Poprawnie: 265/412 [64%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« W prostokącie przekątne długości d przecinają
się pod kątem \alpha.
Wyznacz pole powierzchni tego prostokąta.
Dane
d=8
\alpha=45^{\circ}
\alpha=45^{\circ}
Odpowiedź:
P_{\square}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 6. 1 pkt ⋅ Numer: pp-12414 ⋅ Poprawnie: 184/247 [74%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Kwadrat K_2 jest podobny do kwadratu K_1
w skali 4 (zobacz rysunek). Suma pól tych kwadratów jest równa
34.
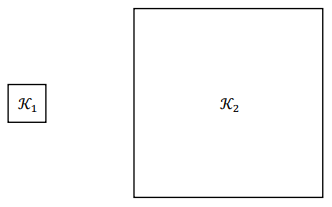

Długość boku kwadratu K_1 jest równa:
Odpowiedzi:
| A. \frac{\sqrt{2}}{3} | B. 4 |
| C. 2 | D. \sqrt{2} |
| E. \frac{\sqrt{2}}{4} | F. 3\sqrt{2} |
| G. \frac{\sqrt{2}}{2} | H. 2 |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20455 ⋅ Poprawnie: 15/76 [19%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Kwadraty ABCD oraz
DEFG mają takie same pola powierzchni
równe 72.
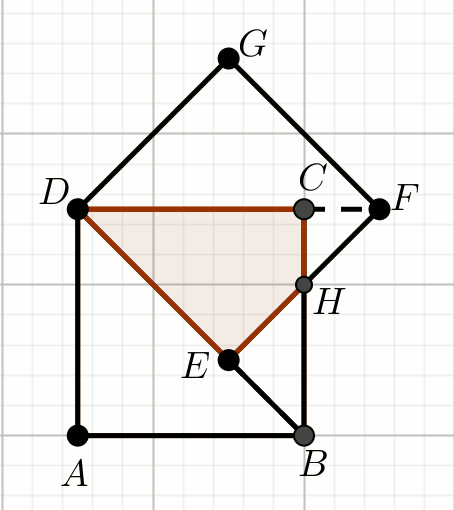

Oblicz pole czworokąta HCDE.
Wynik zapisz w postaci a+b\sqrt{c}. Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 8. 4 pkt ⋅ Numer: pp-30115 ⋅ Poprawnie: 15/61 [24%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Punkty M i N na poniższym
rysunku są środkami boków kwadratu ABCD o boku
długości a.
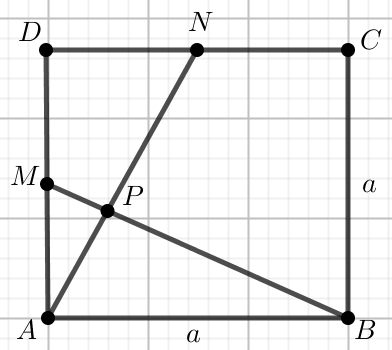

Oblicz miarę stopniową kąta APM.
Dane
a=10
Odpowiedź:
|\sphericalangle APM|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (2 pkt)
Oblicz pole czworokąta BCNP.
Odpowiedź:
| P_{BCNP}= | |
| Zadanie 9. 4 pkt ⋅ Numer: pp-30116 ⋅ Poprawnie: 26/107 [24%] | Rozwiąż |
Podpunkt 9.1 (4 pkt)
Brązowy czworokąt na rysunku jest kwadratem, w którym niebieskie odcinki łączą
wierzchołki ze środkami bokow:
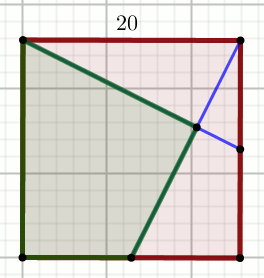

Uzasadnij, że na zielonym czworokącie można opisać okrąg.
Oblicz pole powierzchni zielonego czworokąta.
Odpowiedź:
P=
(wpisz liczbę całkowitą)
| Zadanie 10. 4 pkt ⋅ Numer: pp-30117 ⋅ Poprawnie: 12/86 [13%] | Rozwiąż |
Podpunkt 10.1 (4 pkt)
« Przekątne prostokąta ABCD o bokach długości
a i b przecinają się w
punkcie P pod kątem
|\sphericalangle APD|=30^{\circ}.
Pole trójkąta APD jest równe
p.
Oblicz pole powierzchni kwadratu o boku długości a+b.
Dane
p=100
Odpowiedź:
P_{\square}=
(wpisz liczbę całkowitą)