⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Pole powierzchni kwadratu i prostokąta
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- pole powierzchni kwadratu
- pole powierzchni prostokąta
- wzory na pole
- własności pola powierzchni
| Zadanie 1. 2 pkt ⋅ Numer: pr-20143 ⋅ Poprawnie: 11/24 [45%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
Czworokąt na rysunku jest prostokątem:
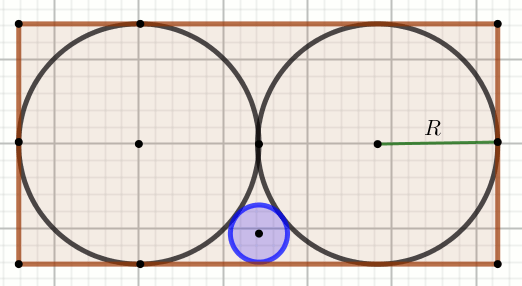
Oblicz długość promienia niebieskiego okręgu.
Dane
R=52
Odpowiedź:
r=
(wpisz liczbę całkowitą)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20144 ⋅ Poprawnie: 43/84 [51%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
» Czworokąt na rysunku jest prostokątem:
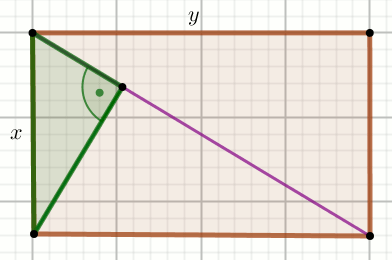
Oblicz pole powierzchni zielonego trójkąta.
Dane
x=10
y=24
y=24
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20145 ⋅ Poprawnie: 36/77 [46%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Czworokąt na rysunku jest prostokątem:
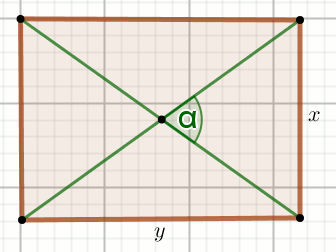
Oblicz \sin\alpha.
Dane
x=10
y=24
y=24
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20146 ⋅ Poprawnie: 19/29 [65%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Pole powierzchni prostokąta wynosi 528. Długość
jednego boku tego prostokąta zmniejszono o 6,
a długość drugiego boku zwiększono o 9. Wówczas
okazało się, że pole powierzchni prostokąta nie uległo zmianie.
Jaką długość miał krótszy bok tego prostokąta?
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
Jaką długość miał dłuższy bok tego prostokąta?
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 5. 4 pkt ⋅ Numer: pr-30113 ⋅ Poprawnie: 6/17 [35%] | Rozwiąż |
Podpunkt 5.1 (4 pkt)
Czworokąt na rysunku jest prostokątem:
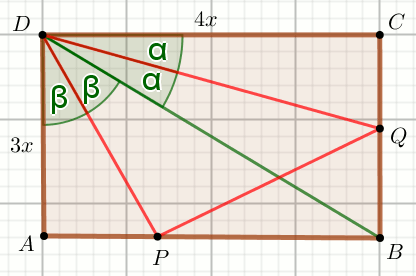
Oblicz \frac{P_{ABCD}}{P_{PQD}}.
Odpowiedź:
| \frac{P_{ABCD}}{P_{PQD}}= | |
| Zadanie 6. 4 pkt ⋅ Numer: pr-30114 ⋅ Poprawnie: 11/26 [42%] | Rozwiąż |
Podpunkt 6.1 (4 pkt)
» Czworokąt na rysunku jest prostokątem:
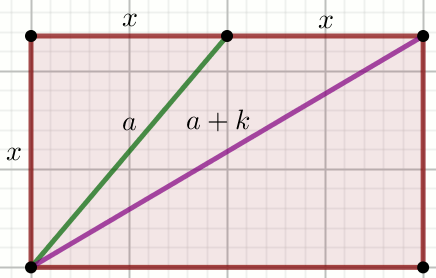
Oblicz jego pole powierzchni.
Dane
k=7
Odpowiedź:
| P_{\square}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 7. 4 pkt ⋅ Numer: pr-30115 ⋅ Poprawnie: 9/28 [32%] | Rozwiąż |
Podpunkt 7.1 (4 pkt)
Czworokąt na rysunku jest prostokątem:
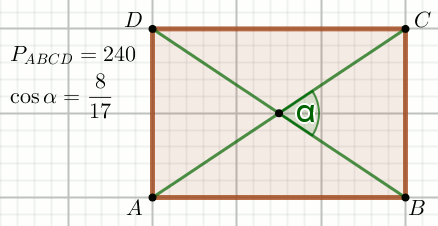
Jaki obwód ma ten prostokąt?
Odpowiedź:
L_{\square}=
(wpisz liczbę całkowitą)
| Zadanie 8. 4 pkt ⋅ Numer: pr-30116 ⋅ Poprawnie: 25/45 [55%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Czworokąt na rysunku jest prostokątem:
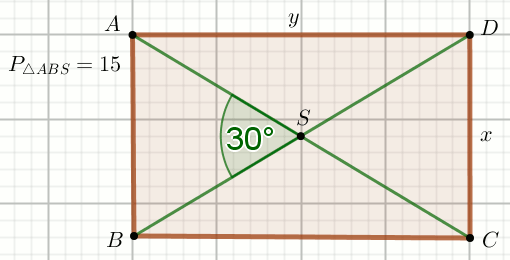
Oblicz jego pole powierzchni.
Odpowiedź:
P_{\square}=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Oblicz długość przekątnej tego prostokąta.
Odpowiedź:
|BD|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.3 (1 pkt)
Oblicz (x+y)^2.
Odpowiedź:
(x+y)^2=
(wpisz liczbę całkowitą)
| Zadanie 9. 4 pkt ⋅ Numer: pr-30889 ⋅ Poprawnie: 15/57 [26%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Dany jest kwadrat ABCD o boku a długości 2.
Punkt E dzieli bok CD w stosunku
|DE|:|EC|=2:1. Przekątna BD dzieli
trójkąt ACE na dwie figury: AGF oraz
CEFG (zobacz rysunek).
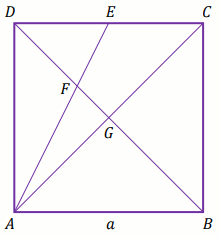
Oblicz pole trójkąta AGF.
Odpowiedź:
| P_{\triangle AGF}= | |
Podpunkt 9.2 (2 pkt)
Oblicz pole czworokąta CEFG.
Odpowiedź:
| P_{\square CEFG}= | |