Pole powierzchni trapezu
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
pole powierzchni trapezu
wzory na pole trapezu
własności pola powierzchni
Zadanie 1. 2 pkt ⋅ Numer: pr-20153 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 1.1 (2 pkt)
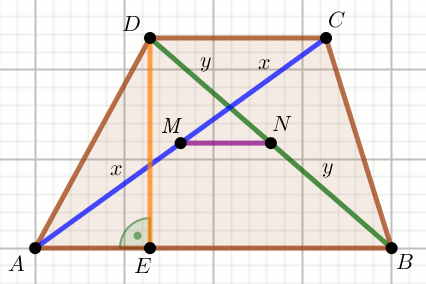
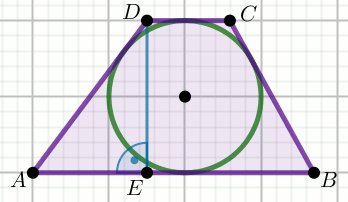
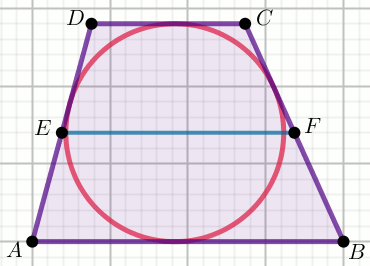
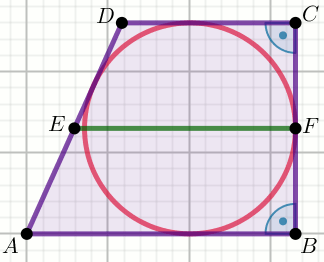
» Czworokąt na rysunku jest trapezem:
Oblicz pole powierzchni tego trapezu.
Dane
|CD|=42 |MN|=24 |DE|=54
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 2. 2 pkt ⋅ Numer: pr-20163 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 2.1 (1 pkt)
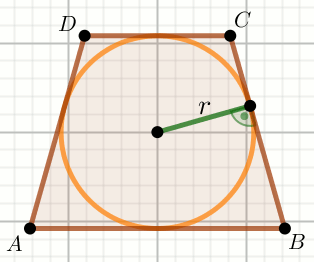
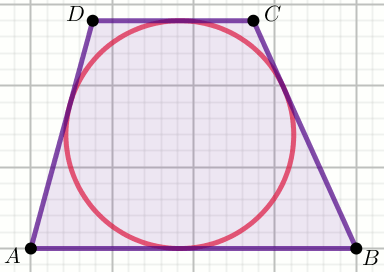
» Czworokąt na rysunku jest trapezem równoramiennym:
Oblicz długość ramienia tego trapezu.
Dane
r=8=8.000000000000000 P_{ABCD}=320=320.000000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 2.2 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 3. 2 pkt ⋅ Numer: pr-20164 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 3.1 (2 pkt)
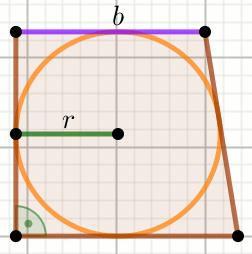
» Czworokąt na rysunku jest trapezem:
Oblicz pole powierzchni tego trapezu.
Dane
r=125=125.000000000000000 b=\frac{375}{2}=187.500000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 4. 2 pkt ⋅ Numer: pr-20165 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 4.1 (2 pkt)
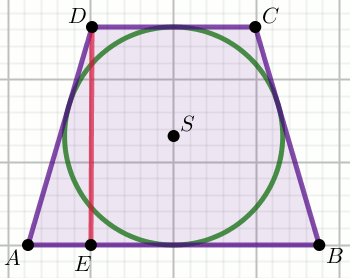
Pole powierzchni trapezu równoramiennego o kącie ostrym
\alpha=30^{\circ} jest równe
\frac{242}{3} :
Oblicz długość promienia tego okręgu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 5. 2 pkt ⋅ Numer: pr-20166 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 5.1 (1 pkt)
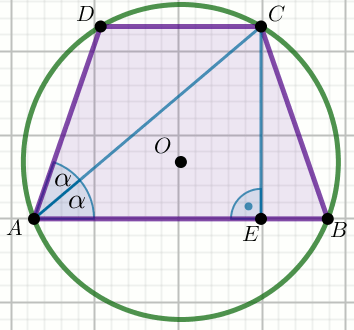
Na trapezie
ABCD , w którym
|CE|=13\sqrt{3}
i
|AB|=2\cdot |CD| , opisano okrąg:
Oblicz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (1 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 6. 2 pkt ⋅ Numer: pr-20167 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 6.1 (1 pkt)
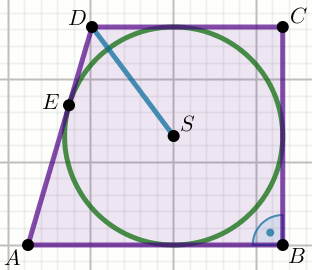
W trapezie prostokątnym
ABCD dane są:
|AB|=60 ,
|BC|=11 i
|CD|=15 :
Wyznacz odległość punktu O od dłuższej podstawy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Wyznacz odległość punktu
O od krótszego ramienia.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 7. 2 pkt ⋅ Numer: pr-20168 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 7.1 (2 pkt)
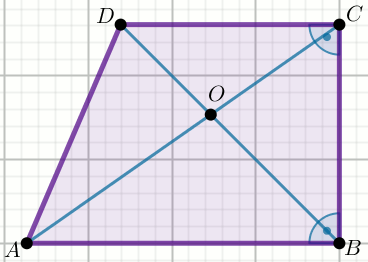
« Przedstawiony na rysunku czworokąt jest trapezem prostokątnym, w którym:
P_{\triangle ABO}:P_{\triangle CDO}=25:4 oraz
P_{\triangle BCO}=10 :
Wyznacz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 8. 2 pkt ⋅ Numer: pr-20169 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 8.1 (2 pkt)
» Przedstawiony na rysunku czworokąt jest trapezem, w którym
|AB|=24 ,
|CD|=12 ,
|AC|=30 i
|BD|=15 :
Oblicz P_{ABCD} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 9. 2 pkt ⋅ Numer: pr-20170 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 9.1 (1 pkt)
W trapez prostokątny
ABCD o stosunku boków
|BC|:|AD|=40:41 wpisano okrąg o promieniu
długości
24 :
Oblicz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 10. 2 pkt ⋅ Numer: pr-20154 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 10.1 (1 pkt)
» Czworokąt
ABCD jest trapezem, w którym
|AD|=10 ,
|BC|=17 ,
oraz
|DE|:|AE|=\frac{4}{3} . W trapez ten wpisano okrąg:
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (1 pkt)
Oblicz
P_{\triangle BCD} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 11. 2 pkt ⋅ Numer: pr-20155 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 11.1 (2 pkt)
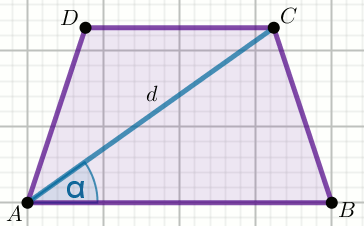
W trapezie równoramiennym przekątna
AC ma długość
d=34 i tworzy z dłuższą podstawą
AB
kąt o mierze
\alpha=45^{\circ} :
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 12. 2 pkt ⋅ Numer: pr-20156 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 12.1 (2 pkt)
» W trapez równoramienny o kącie rozwartym
\alpha takim,
\cos\alpha=-\frac{16}{65} i polu powierzchni
P=16380 , wpisano okrąg:
Oblicz długość ramienia tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 13. 2 pkt ⋅ Numer: pr-20157 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 13.1 (2 pkt)
Na trapezie
ABCD o polu powierzchni
P=588\sqrt{3} ,
w którym
|AB|=2\cdot |CD| , opisano okrąg:
Oblicz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 14. 2 pkt ⋅ Numer: pr-20158 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 14.1 (1 pkt)
W trapez równoramienny o podstawach długości
98 i
50 można wpisać okrąg.
Oblicz długość wysokości tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 15. 2 pkt ⋅ Numer: pr-20159 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 15.1 (2 pkt)
» Czworokąt
ABCD jest trapezem, w którym
|AD|=10 ,
|BC|=17 ,
oraz
|DE|:|AE|=\frac{4}{3} . W trapez ten wpisano okrąg:
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 16. 2 pkt ⋅ Numer: pr-20160 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 16.1 (2 pkt)
» Pole powierzchni trapezu
T_1 wynosi
P . Trapez
T_2 ma
obie podstawy dłuższe o
d i wysokość krótszą o
p . Pola pól powierzchni trapezów
T_1 i
T_2 są sobie równe.
Oblicz wysokość trapezu T_1 .
Dane
P=\frac{35}{12}=2.91666666666667 d=1=1.00000000000000 p=\frac{1}{3}=0.33333333333333
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 17. 2 pkt ⋅ Numer: pr-20161 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 17.1 (2 pkt)
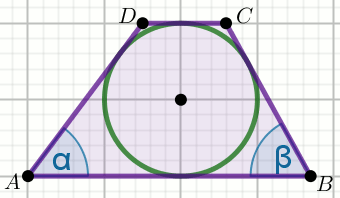
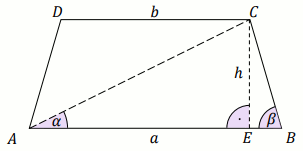
» Pole powierzchni trapezu pokazanego na rysunku jest równe
108 , a kąty
\alpha
i
\beta spełniają warunki
\sin\alpha=\frac{4}{5} i
\cos\beta=\frac{15}{17} :
Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 18. 2 pkt ⋅ Numer: pr-20162 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 18.1 (1 pkt)
Punkty
E i
F są środkami
ramion o długościach
|AD|=10 i
|BC|=17 trapezu, w który
wpisano okrąg, i w którym
\frac{P_{EFCD}}{P_{ABFE}}=\frac{11}{25} .
Oblicz długość krótszej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.2 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 19. 2 pkt ⋅ Numer: pr-20768 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 19.1 (1 pkt)
« Promień okręgu wpisanego w trapez prostokątny ma długość
30 , a kąt rozwarty tego trapezu
\alpha spełnia warunek
\cos\alpha=-\frac{11}{61} .
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 20. 4 pkt ⋅ Numer: pr-20806 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 20.1 (2 pkt)
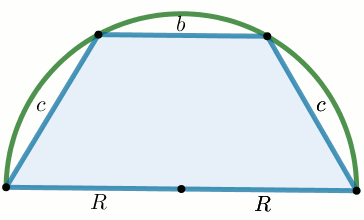
(2 pkt) W półkole o promieniu długości
R
wpisano trapez o obwodzie długości
L ,
którego wysokość jest liczbą niewymierną, a dłuższa podstawa trapezu
jest średnicą tego półkola.
Wyznacz długość ramienia tego trapezu.
Dane
R=100 L=496
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (2 pkt)
(2 pkt) Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 21. 4 pkt ⋅ Numer: pr-30124 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 21.1 (4 pkt)
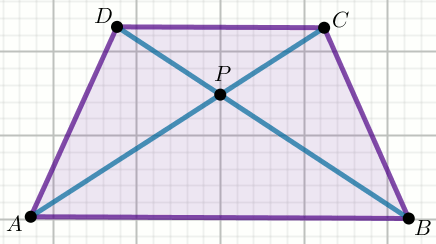
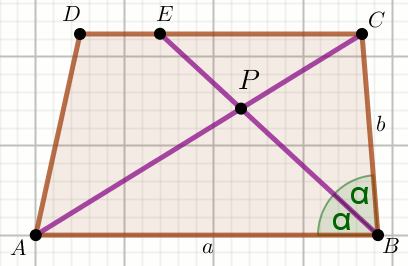
Czworokąt na rysunku jest trapezem, w którym
P_{ABED}=2\cdot P_{ABP} :
Oblicz |CD| .
Dane
a=30 b=18
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 22. 4 pkt ⋅ Numer: pr-30127 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 22.1 (2 pkt)
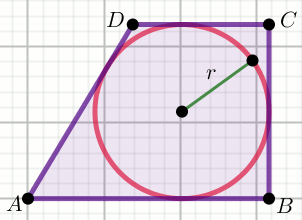
« Czworokąt na rysunku jest trapezem, w którym
|AD|=4\sqrt{6}
oraz
\cos\alpha=\frac{4\sqrt{2}}{7} . W trapez ten wpisano okrąg:
Wyznacz promień okręgu wpisanego w ten czworokąt.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 22.2 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 23. 4 pkt ⋅ Numer: pr-30128 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 23.1 (2 pkt)
« Kąt ostry trapezu równoramiennego wpisanego w okrąg, którego dłuższa
podstawa jest średnicą tego okręgu o promieniu
r ,
ma miarę
60^{\circ} .
Wyznacz pole powierzchni tego trapezu.
Dane
r=\frac{7\sqrt{2}}{4}=2.47487373415292
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 23.2 (2 pkt)
Wyznacz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 24. 4 pkt ⋅ Numer: pr-30129 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 24.1 (1 pkt)
« W trapezie prostokątnym
ABCD dane są
|AB|=12 i
|CD|=4 , a punkty
E i
F są środkami jego ramion.
W trapez ten wpisano okrąg:
Oblicz |EF| .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 24.2 (1 pkt)
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 24.3 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 25. 4 pkt ⋅ Numer: pr-30130 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 25.1 (1 pkt)
« Pole powierzchni trapezu, w który wpisano okrąg, jest równe
108 , a jego ramiona mają długość
|AD|=10 i
|BC|=17 :
Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 25.2 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 25.3 (2 pkt)
Oblicz pole powierzchni najmniejszego z trójkątów, na jakie trapez dzielą
jego przekątne.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 26. 4 pkt ⋅ Numer: pr-30131 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 26.1 (1 pkt)
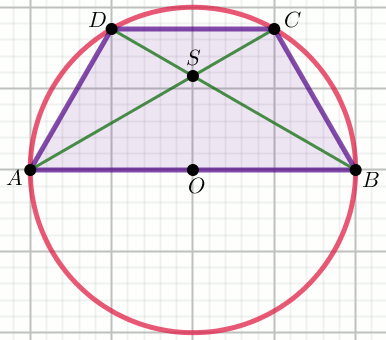
» Na trapezie
ABCD opisano okrąg o środku w punkcie
O , w taki sposób, że dłuższa
podstawa tego trapezu jest średnicą okręgu. Odcinki
AD i
OC mają równą długość wynoszącą
12\sqrt{5} :
Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 26.2 (1 pkt)
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 26.3 (1 pkt)
Wyznacz
P_{\triangle ABS} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 26.4 (1 pkt)
Wyznacz długość promienia okręgu wpisanego w trójkąt
ABS .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 27. 4 pkt ⋅ Numer: pr-30132 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 27.1 (2 pkt)
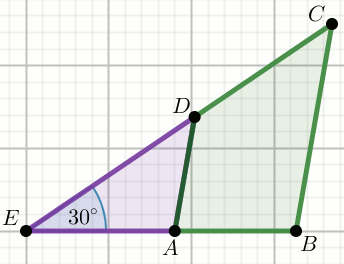
«« Zielony czworokąt na rysunku jest trapezem, w którym:
AD\parallel BC ,
|AB|=28 ,
|CD|=28\sqrt{3} ,
|DE|=\sqrt{3} :
Oblicz pole powierzchni tego czworokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 27.2 (2 pkt)
Oblicz długość obwodu tego czworokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 28. 4 pkt ⋅ Numer: pr-30133 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 28.1 (2 pkt)
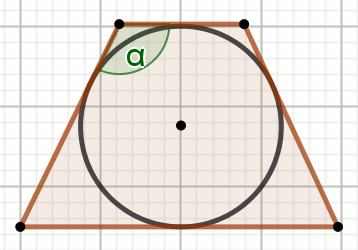
» Czworokąt na rysunku jest trapezem równoramiennym, w którym:
|DE|:|AD|=\frac{24}{25} oraz
|CD|=72 :
Oblicz długość wysokości tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 28.2 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 29. 4 pkt ⋅ Numer: pr-30134 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 29.1 (2 pkt)
« Na okręgu opisano trapez równoramienny, którego przekątna ma długość
\sqrt{3281} . Obwód tego trapezu ma długość
164 .
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 29.2 (2 pkt)
Oblicz cosinus kąta rozwartego tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 30. 4 pkt ⋅ Numer: pr-30125 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 30.1 (2 pkt)
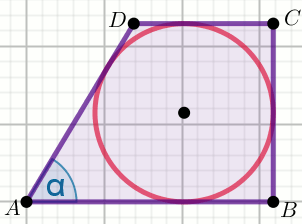
Czworokąt na rysunku jest trapezem, w który wpisano okrąg styczny do dłuższego ramienia
AB trapezu w punkcie
E .
Odcinek
AE ma długość
2 ,
zaś odcinek
DS długość
\sqrt{15} :
Oblicz długość wyskości tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 30.2 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 31. 4 pkt ⋅ Numer: pr-30126 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 31.1 (2 pkt)
«« Trapez
ABCD jest równoramienny. Jego przekątna o
długości
130 tworzy z dłuższą podstawą trapezu
kąt o mierze
\alpha taki, że
\sin\alpha=\frac{16}{65} :
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 31.2 (2 pkt)
W trapez ten można wpisać okrąg.
Oblicz długość krótszej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 32. 5 pkt ⋅ Numer: pr-31022 ⋅ Poprawnie: 0/1 [0%]
Rozwiąż
Podpunkt 32.1 (1 pkt)
Dany jest trapez
ABCD o podstawach
AB i
CD , w którym
|AB|>|CD| oraz ramię
BC ma długość
\frac{25}{4} . Na tym
trapezie opisano okrąg o promieniu
R=\frac{125}{24} . Miary kątów
BAC i
ABC tego trapezu spełniają warunek
\frac{\sin\sphericalangle BAC}{\sin\sphericalangle ABC}=\frac{5}{8} .
Oblicz
\sin\alpha .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 32.2 (1 pkt)
Oblicz wysokość trapezu
h .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 32.3 (1 pkt)
Oblicz długość przekątnej
AC .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 32.4 (1 pkt)
Oblicz długość podstawy
AB .
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 32.5 (1 pkt)
Oblicz pole trapezu
ABCD .
Odpowiedź:
(wpisz dwie liczby całkowite)
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm