⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Własności funkcji wykładniczej. Wykres funkcji wykładniczej
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- wykres funkcji wykładniczej
- własności funkcji wykładniczej
- monotoniczność funkcji wykładniczej
| Zadanie 1. 1 pkt ⋅ Numer: pr-10161 ⋅ Poprawnie: 84/145 [57%] | Rozwiąż |
Podpunkt 1.1 (0.2 pkt)
» Zbiorem wartości funkcji f(x)=\left|a+5^{3-x}\right|
jest zbiór postaci:
Dane
a=-6
Odpowiedzi:
| A. \langle p, q\rangle | B. (-\infty, p\rangle |
| C. (p,+\infty) | D. (p, q) |
| E. \langle p,+\infty) | F. (-\infty, p) |
Podpunkt 1.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 1 pkt ⋅ Numer: pr-10162 ⋅ Poprawnie: 69/124 [55%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt P=\left(x_0,\frac{1}{y_0}\right) należy do
wykresu funkcji wykładniczej określonej wzorem y=a^x.
Do wykresu tej funkcji należy też punkt:
Dane
x_0=10
y_0=32
y_0=32
Odpowiedzi:
| A. \left(11,\frac{1}{16}\right) | B. \left(9,\frac{\sqrt{2}}{32\sqrt{2}}\right) |
| C. \left(9,\frac{1}{64}\right) | D. \left(11,\frac{1}{32\sqrt{2}}\right) |
| Zadanie 3. 1 pkt ⋅ Numer: pr-10163 ⋅ Poprawnie: 14/21 [66%] | Rozwiąż |
Podpunkt 3.1 (0.2 pkt)
Dana jest funkcja określona wzorem f(x)=\frac{1}{0,6^{|x|}}+b.
Zbiór ZW_f ma postać:
Dane
b=-6
Odpowiedzi:
| A. (-\infty, p)\cup(q,+\infty) | B. (-\infty, p\rangle |
| C. \langle p,+\infty) | D. \langle p, q\rangle |
| E. (-\infty, p) | F. (p,+\infty) |
Podpunkt 3.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych
tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 1 pkt ⋅ Numer: pr-10165 ⋅ Poprawnie: 43/50 [86%] | Rozwiąż |
Podpunkt 4.1 (0.2 pkt)
Dziedziną funkcji określonej wzorem
g(x)=\frac{3\sqrt{3}}{\sqrt{\left(\frac{1}{a}\right)^x-b}}
jest zbiór postaci:
Dane
a=4
b=64
b=64
Odpowiedzi:
| A. (p, q) | B. (p,+\infty) |
| C. \langle p, q\rangle | D. (-\infty, p\rangle |
| E. (-\infty, p) | F. \langle p,+\infty) |
Podpunkt 4.2 (0.8 pkt)
Zapisz tę dziedzinę w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych
tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 1 pkt ⋅ Numer: pr-10166 ⋅ Poprawnie: 16/39 [41%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Do wykresu funkcji określonej wzorem g(x)=-\frac{a^x}{b} należą
punkty P=(-2,4) i Q=(-1,3).
Wówczas:
Odpowiedzi:
| A. a-b=3 | B. a\cdot b=-3 |
| C. a-b=1\frac{7}{36} | D. a\cdot b=-1\frac{11}{16} |
| Zadanie 6. 2 pkt ⋅ Numer: pr-20326 ⋅ Poprawnie: 6/16 [37%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Dana jest funkcja
f(x)=
\begin{cases}
3^{-x} \text{, dla } x \lessdot 0 \\
-(x+a)^2+b \text{, dla } x\geqslant 0
\end{cases}
.
Ustal liczbę rozwiąząń równania f(x)=m w zależności
od wartości parametru m.
Podaj długość przedziału tych wartości m, dla których równanie to ma dokładnie trzy rozwiązania.
Dane
a=-5
b=26
b=26
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Podaj największą wartość m, dla której równanie ma
dokładnie dwa rozwiązania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pr-20327 ⋅ Poprawnie: 6/10 [60%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Dla jakich wartości parametru m równanie
\left(\frac{\sqrt{5}}{5}\right)^{3x}=2^{am+b}
ma rozwiązanie dodatnie?
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Dane
a=2
b=1
b=1
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20328 ⋅ Poprawnie: 5/27 [18%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Dla jakich wartości parametru m równanie
2x+a=2^{m-1}
ma rozwiązanie dodatnie?
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Dane
a=128
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 2 pkt ⋅ Numer: pr-20500 ⋅ Poprawnie: 13/33 [39%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Punkt P=\left(p,\frac{1}{q}\right)
należy do wykresu funkcji wykładniczej f(x)=a^x.
Oblicz wartość tej funkcji dla argumentu
\frac{m}{2}.
Zakoduj kolejno trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.
Dane
p=8
q=625
m=-1
q=625
m=-1
Odpowiedź:
Wpisz odpowiedź:
(wpisz odpowiedź tekstową)
| Zadanie 10. 4 pkt ⋅ Numer: pr-30228 ⋅ Poprawnie: 22/97 [22%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Naszkicuj wykresy funkcji f(x)=2^x i
g(x)=|f(x-a)-b|.
Podaj najmniejszą wartość funkcji g w przedziale \langle p,q\rangle.
Dane
a=-3
b=8
p=-3
q=2
b=8
p=-3
q=2
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
Podaj największą wartość funkcji g w tym przedziale.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.3 (1 pkt)
Podaj miejsce zerowe funkcji g.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 4 pkt ⋅ Numer: pr-30232 ⋅ Poprawnie: 3/12 [25%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Dane jest równanie
\left|\frac{a^{x+1}-1}{a^x}\right|=m z parametrem
m\in\mathbb{R}.
Wyznacz najmniejszą wartość m, dla której równanie to ma dokładnie jedno rozwiązanie.
Dane
a=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Podaj najmniejszą dodatnią wartość m, dla której
równanie ma dokładnie jedno rozwiązanie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.3 (2 pkt)
Wyznacz zbiór tych wartości parametru m, dla których
równanie to ma dokładnie dwa rozwiązania.
Zbiór ten zapisz w postaci przedziału. Podaj długość tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. 3 pkt ⋅ Numer: pr-30233 ⋅ Poprawnie: 13/30 [43%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Dana jest funkcja g(x)=|2^{x-1}-3| oraz
x_0=\log_{2}{a}+\log_{2}{a}\cdot \log_{a}{2}.
Oblicz g(x_0).
Dane
a=64
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (1 pkt)
Wyznacz te wartości x, dla których funkcja
g przyjmuje wartości większe od
g(x_0).
Podaj najmniejszą dodatnią liczbę całkowitą, która do tego zbioru nie należy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.3 (1 pkt)
Podaj największą dodatnią liczbę, która do tego zbioru nie należy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. 4 pkt ⋅ Numer: pr-30234 ⋅ Poprawnie: 5/22 [22%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
« Wykres funkcji f(x)=c^x zawiera punkt
A=(2\log_{2}{a},b).
Podaj c.
Dane
a=5
b=25
q=3
b=25
q=3
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (2 pkt)
Funkcja g określona jest wzorem
g(x)=|f(x+1)-q|.
Naszkicuj wykres funkcji g i na jego podstawie ustal, dla których m równanie g(x)=m ma dokładnie jedno rozwiązanie.
Naszkicuj wykres funkcji g i na jego podstawie ustal, dla których m równanie g(x)=m ma dokładnie jedno rozwiązanie.
Ile liczb całkowitych m\in\langle -10,10\rangle spełnia warunki zadania?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.3 (1 pkt)
Podaj najmniejszą dodatnią wartość m, która spełnia
warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. 4 pkt ⋅ Numer: pr-30235 ⋅ Poprawnie: 8/50 [16%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
«« Wykres funkcji f(x)=a^x zawiera punkt
A=\left(-\frac{3}{2},\frac{1}{8}\right).
Podaj a.
Dane
b=5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (2 pkt)
Funkcja g określona jest wzorem
g(x)=|b-f(x-1)|.
Naszkicuj wykres funkcji g i na jego podstawie ustal, dla których m równanie g(x)=m ma dokładnie jedno rozwiązanie.
Naszkicuj wykres funkcji g i na jego podstawie ustal, dla których m równanie g(x)=m ma dokładnie jedno rozwiązanie.
Ile liczb całkowitych m\in\langle -10,10\rangle spełnia warunki zadania?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.3 (1 pkt)
Podaj najmniejszą dodatnią wartość m, która spełnia
warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. 4 pkt ⋅ Numer: pr-30236 ⋅ Poprawnie: 4/9 [44%] | Rozwiąż |
Podpunkt 15.1 (2 pkt)
Dane są funkcje f(x)=2^{ax-4} i
g(x)=5-\left(\frac{1}{2}\right)^{ax-6}.
Rozwiąż nierówność f(x)\leqslant g(x).
Jaka największa liczba spełnia tę nierówność?
Dane
a=8
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (2 pkt)
Podaj najmniejszą liczbę spełniającą tę nierówność.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. 4 pkt ⋅ Numer: pr-30237 ⋅ Poprawnie: 6/22 [27%] | Rozwiąż |
Podpunkt 16.1 (2 pkt)
« Dane są funkcje f(x)=1-2^{x+a} i
g(x)=x^2+(2a-2)x+a^2-2a.
Rozwiąż graficznie nierówność f(x)\leqslant g(x).
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich tych końców przedziałów, które są liczbami.
Dane
a=-4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (2 pkt)
Podaj sumę kwadratów wszystkich tych końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. 4 pkt ⋅ Numer: pr-30238 ⋅ Poprawnie: 5/24 [20%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
« Naszkicuj wykres funkcji f(x)=\left|a^{x+1}-b\right|.
Podaj największą wartość tej funkcji w przedziale \langle -1,2\rangle.
Dane
a=7
b=8
b=8
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (1 pkt)
Podaj najmniejszą wartość tej funkcji w przedziale
\langle -1,2\rangle.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.3 (2 pkt)
Dla jakich wartości parametru m równanie
f(x)=m ma dwa rozwiązania?
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. 4 pkt ⋅ Numer: pr-30239 ⋅ Poprawnie: 4/13 [30%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
» Naszkicuj wykres funkcji
f(x)=\left|a^{2-x}-b\right|.
Podaj największą wartość tej funkcji w przedziale \langle -1,2\rangle.
Dane
a=7
b=8
b=8
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.2 (1 pkt)
Podaj najmniejszą wartość tej funkcji w przedziale
\langle -1,2\rangle.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.3 (2 pkt)
Dla jakich wartości parametru m równanie
f(x)=m ma dwa rozwiązania?
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 19. 4 pkt ⋅ Numer: pr-30229 ⋅ Poprawnie: 2/14 [14%] | Rozwiąż |
Podpunkt 19.1 (2 pkt)
Dane są funkcje f(x)=-m^x+a oraz
g(x)=m^{|x-1|}+a.
Punkt B=(2, 0) należy do wykresu funkcji
f.
Podaj m.
Dane
a=7
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (1 pkt)
Dla jakich wartości parametru p równanie
g(x)=p ma rozwiązania.
Podaj najmniejsze możliwe p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.3 (1 pkt)
Podaj najmniejszą całkowitą wartość parametru p,
dla której równanie g(x)=p ma dwa rozwiązania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 20. 6 pkt ⋅ Numer: pr-30230 ⋅ Poprawnie: 1/39 [2%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
« Dane jest równanie (k-1)^2x^2+(k-2)x+1=0, gdzie
k\neq -1. Funkcja g
przyporządkowuje liczbie k liczbę
g(k)=2^{\frac{1}{x_1}+\frac{1}{x_2}}, gdzie
x_1,x_2 są różnymi pierwiastkami tego równania.
Wyznacz D_g=(a, b).
Podaj a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (1 pkt)
Podaj b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.3 (2 pkt)
Zbiorem wartości funkcji g jest przedział
ZW_g=(\sqrt[3]{c},d).
Podaj c.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.4 (2 pkt)
Podaj d.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 21. 4 pkt ⋅ Numer: pr-30231 ⋅ Poprawnie: 23/62 [37%] | Rozwiąż |
Podpunkt 21.1 (2 pkt)
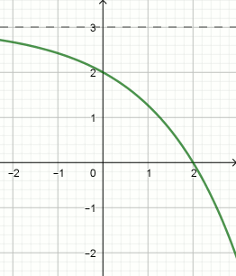
Na rysunku pokazano wykres funkcji f(x)=-a^x+3.
Wyznacz a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 21.2 (2 pkt)
Naszkicuj wykres funkcji
g(x)=a^{|x+5|}-8.
Podaj najmniejszą wartość funkcji g.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)