Rozwiązywanie równań wykładniczych

 Rozwiąż równanie 7\cdot 4^{x+1-a}-2^{2x+3-2a}=26+7\cdot 4^{x-a} .

Podaj największe rozwiązanie tego równania.

 Wiadomo, że 8^x=27 oraz 2^{x-2ay}=27.

Zapisz liczbę y w postaci p\cdot \log_{2}{\frac{1}{3}}. Podaj p.

 Rozwiąż równanie 4\cdot 2^{x+a}=4^{x-6+a} .

Podaj największe z rozwiązań.

 « Rozwiąż równanie 9^{x^2-2ax+5+a^2}=27^{4x-2-4a}.

Podaj najmniejsze z rozwiązań tego równania.

 Podaj największe z rozwiązań tego równania.

 Rozwiąż równanie \left(\frac{2}{5}\right)^{x+a}\cdot 2,5^{-x+3-a}=\frac{4}{25} .

Podaj największe z rozwiązań.

 Rozwiąż równanie 9^{\frac{x-a}{2}-1}+3^{x-a}=7290 .

Podaj największe z rozwiązań.

 W chwili początkowej (t=0) filiżanka z gorącą kawą znajduje się w pokoju, a temperatura tej kawy jest równa 86^{\circ}C. Temperatura w pokoju (temperatura otoczenia) jest stała i równa 18^{\circ}C. Temperatura T tej kawy zmienia się w czasie zgodnie z zależnością T(t)=(T_p-T_z)\cdot k^{-t}+T_z dla t\geqslant 0 gdzie:

• T – temperatura kawy wyrażona w stopniach Celsjusza,
• t – czas wyrażony w minutach, liczony od chwili początkowej,
• T_p – temperatura początkowa kawy wyrażona w stopniach Celsjusza,
• T_z – temperatura otoczenia wyrażona w stopniach Celsjusza,
• k – stała charakterystyczna dla danej cieczy.

Po 10 minutach, licząc od chwili początkowej, kawa ostygła do temperatury 52^{\circ}C.

Oblicz temperaturę tej kawy po następnych pięciu minutach.

 W chwili początkowej (t=0) zainicjowano pewną reakcję chemiczną, w której brał udział związek A. W wyniku tej reakcji masa m związku A zmieniała się w czasie zgodnie z zależnością m(t)=a\cdot 2^{-0.25\cdot t}+b dla t\geqslant 0 gdzie:

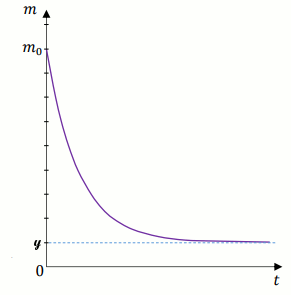
• m – masa związku A wyrażona w gramach,
• t – czas wyrażony w sekundach (liczony od chwili t=0),
• a,b – współczynniki liczbowe.

Masa początkowa związku A (tj. masa w chwili t=0) była równa m_0 gramów. Po osiągnięciu stanu równowagi (tj. gdy t\rightarrow \infty) masa tego związku była równa \frac{1}{9} jego masy początkowej, czyli y=\frac{1}{9}m_0 (zobacz rysunek).

Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało \frac{4}{9} masy początkowej tego związku.